How String Theory Could Unify the Universe with Quantum Gravity
When it comes to understanding the deepest workings of the universe, much of modern physics postulates that reality consists of elementary particles like quarks, gluons, and photons. But some think that a far more profound theory could bring everything together—and that theory is String Theory. From gravity to the particles that form matter, the potential of this theory to explain the fundamental nature of the cosmos is nothing short of revolutionary.
In this article, we will explore the basic concepts of String Theory and its aspirations to become a “Theory of Everything (ToE).” Informed by the work I undertook at Harvard University and my ongoing interest in quantum theory, this discussion aims to break down the questions that both inspire and challenge this exciting theory in physics.
Why Strings? The Origins of String Theory
So, how did String Theory emerge as a possible solution to one of the most vexing issues in physics today—that is, incorporating gravity into quantum mechanics?
The theory first gained traction in the late 1960s when physicists were studying the strong nuclear force, which governs how quarks bind within protons and neutrons. Early investigations revealed peculiar properties, particularly in hadrons (collections of quarks), which suggested that quarks might be connected by small, vibrating “strings” composed of strong nuclear energy. In this version, strings could potentially explain these bonds through their vibrational characteristics.
Although this early attempt focused on understanding the strong force, it soon morphed into something much larger—a hypothetical explanation for all particles and forces in the universe, including gravity, which has long resisted quantum description through the standard model of particle physics.
What Makes String Theory Different?
What’s unique about String Theory is that rather than treating particles as 0-dimensional points, it suggests they are 1-dimensional objects—strings. These strings vibrate at specific frequencies, and it’s these vibrational modes that determine fundamental properties such as particle mass and spin. Picture a guitar string: depending on how it vibrates, different notes (or in this case, particles) emerge.
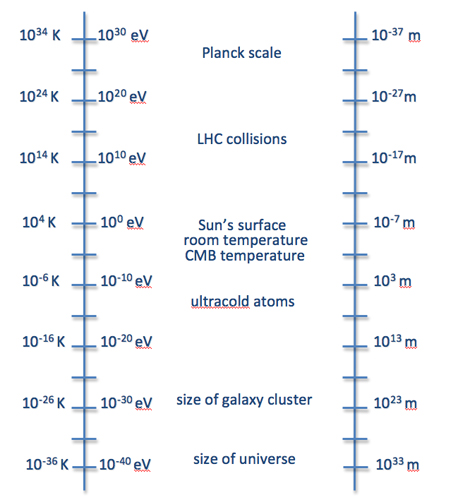
But here’s the catch: these strings are extraordinarily small—at the Planck scale, about 10-35 meters—making them billions of times smaller than anything we can observe today.
A Grand Unified Theory? The Role of Extra Dimensions
In order for String Theory to predict the universe accurately, it requires additional spatial dimensions beyond the three we are familiar with (length, width, height). Initially, the theory needed 26 dimensions to work, but this was refined down to 10 dimensions in what we now call Superstring Theory.
Why so many dimensions? Well, in the world of physics, additional dimensions mean extra “space” for these strings to vibrate in—leading to the rich variety of particles and forces that form the reality we experience. These extra dimensions are theorized to be compactified into incredibly tiny shapes, so we don\u2019t perceive them in our everyday lives. Think of them like tiny loops or folds that are “rolled up” tightly within the structure of space-time itself.
Ed Witten’s introduction of M-theory in 1995 offered a more refined version of the theory, adding an 11th dimension, potentially opening new possibilities for explaining gravitational forces.
Solving the Quantum Gravity Puzzle
But how does String Theory propose to solve the pesky problem of quantum gravity? In the standard model, gravity remains a bit of an outsider. The graviton, a hypothetical quantum of the gravitational field, doesn’t fit neatly with the quantum mechanical descriptions of the other forces (like electromagnetism or the strong nuclear force).
This is where String Theory could step in. One unexpected result in early string models was the appearance of a massless spin-2 particle, which matches the predicted properties of the graviton. Thus, strings could provide an elegant solution to unifying gravity under a quantum framework.
Unlike point particles, which often result in undesired mathematical problems like infinite energies (in the context of gravity), 1-dimensional strings offer a way around these issues. Their extended nature “smooths out” these problematic interactions, offering a more stable theory for describing the gravitational field at quantum scales.
< >
>
Challenges and Controversies
Although String Theory holds an alluring promise of unifying all forces of nature, it is far from proven. One of the big issues is that the theory provides no testable predictions that can currently be verified or falsified with experimentation. In fact, there is estimated to be about 10500 possible “solutions” or configurations of the compact extra dimensions, making it nearly impossible to know which one (if any) describes our universe.
As with many fields in science and technology, including my own work in AI and ML, refining the model is crucial. In our exploration of AI limitations, I discussed the role model refinement plays in achieving real-world use cases. Similarly, for String Theory to go beyond a beautiful, elegant idea and become a staple of scientific fact, physicists will need breakthrough verification—something many are still working toward.
< >
>
Conclusion: The Future of String Theory
Despite its current limitations, String Theory continues to attract some of the brightest minds in the field of theoretical physics. Its elegance, mathematical beauty, and potential applicability to Wolfram’s Theory of Everything and other grand unification concepts make it a compelling road map toward the ultimate understanding of our universe. Whether strings are the fundamental building blocks remains to be seen, but their role in helping to solve the mysteries of quantum gravity keeps them at the forefront of scientific discourse.
As I have found in my journey, from AI and Machine Learning to astronomy with my group of amateur astronomer friends, theories often take time to mature, and may not always have linear paths. String Theory, while still controversial, may one day unlock the final mysteries of our cosmos.
< >
>
Focus Keyphrase: String Theory and Quantum Gravity