Tag Archive for: theoretical physics

Understanding String Theory: The Quest for the Ultimate “Theory of Everything”

The Revolutionary World of String Theory: A Deep Dive into the Fundamentals

In the realm of modern physics, few concepts hold as much allure and controversy as string theory. It is often presented as the leading candidate for a “theory of everything”—a framework that could unify all forces and particles in the universe. Many of us, at some point, have come across the idea of tiny, vibrating strings being the foundational building blocks of the cosmos, but what lies beneath this abstract notion, and what does string theory truly offer?

What is String Theory?

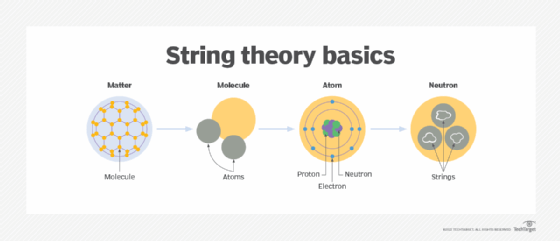
String theory suggests that the most fundamental entities in the universe are not point particles, like electrons or quarks, but one-dimensional “strings” that vibrate at different frequencies. The theory posits that these strings, much like vibrating guitar strings, resonate and define physical properties of particles, such as mass and charge, with their vibrational modes determining what kind of particle they correspond to.

String theory originated in the 1960s as an attempt to describe the strong nuclear force that binds protons and neutrons together. Early investigations revealed intriguing properties in strings—such as the potential existence of a theoretical particle called the graviton, linking string theory directly to quantum gravity. This realization by physicists opened the door for even more ambitious ideas, including the notion that all particles, forces, and even spacetime itself can be explained by vibrating strings—effectively making string theory a viable candidate for a unified theory.

Why Strings? Why Not Something Else?

The introduction of strings came from frustration with the limitations of the Standard Model, a highly successful but incomplete framework for understanding particle physics. The Standard Model predicts many phenomena with striking accuracy but also leaves unanswered questions, such as how gravity and quantum mechanics can coexist, and why the Standard Model requires 19 adjustable parameters to fit experimental data.

String theory promises to reduce these complexities. Using only one parameter—the string tension—string theory hopes to describe all observed particles and forces, including gravity. The reason strings seem so attractive, among other considerations, is that they resolve infinities that emerge in quantum gravitational calculations. In short, where quantum gravity tends to produce mathematical contradictions at small scales, string theory remains consistent by smearing those interactions over tiny one-dimensional loops.

Multiple Dimensions: The Tough Pill to Swallow

However, string theory’s elegance is accompanied by a major complication: to function correctly, it demands the existence of more than our familiar three dimensions of space. Early versions of string theory required up to 26 dimensions, later refined to 10 dimensions in modern superstring theory. Even M Theory, a more recent unifying framework, needs 11 dimensions to describe the universe fully.

How can these extra dimensions exist if we don’t perceive them? String theorists propose that these dimensions are “compactified” – effectively rolled up into tiny shapes so minuscule that we cannot detect them with current technology. If true, these hidden dimensions could reveal profound new insights about how the universe works at its most fundamental level.

<Physics extra dimensions concept>

The Current Status of String Theory

Despite its conceptual strength, string theory remains difficult to test experimentally. A major issue is the immense number of possible configurations—one estimate puts the number of potential solutions at 10 to the power of 500. This vast “landscape” of potential universes makes it nearly impossible to predict which configuration actually describes our own. While its mathematical foundation is beautiful, string theory has yet to produce concrete, experimental predictions.

Nonetheless, it remains one of the leading frameworks for theoretical physicists. Its early unification of forces, gravity, and matter stirred excitement, but as of my writing, we remain at an impasse. Recent articles on my blog, such as The Current Reality and Challenges for AI, have discussed similar growing pains in other technological fields. While string theory holds promise, its scientific future is uncertain.

String Theory’s Philosophical Implications

Even beyond its scientific aspirations, string theory delves into the age-old philosophical question of what reality is made of. If correct, the “strings” at the center of this theory are not composed of anything—much like quantum fields, they represent the most elementary form of existence. In this view, we cannot meaningfully ask what they are “made of” because they represent the baseline, irreducible building blocks of the universe, a concept that seems both simple and deeply profound.

<String theory diagram showing multiple dimensions>

Future Directions and Potential Breakthroughs

The current bottleneck in string theory is similar to the challenges faced by early quantum field theorists. Nearly a century ago, quantum mechanics itself was viewed with similar skepticism, but with time, new technologies and novel approaches might allow tests for string theory’s predictions. Some physicists, holding out hope, believe that indirect tests or mathematical advancements will allow for breakthroughs that could either validate or discard string theory.

<

>

Conclusion

String theory presents both a towering intellectual achievement and a monumental scientific challenge. As I discussed in a recent post on self-driving cars and AI, introducing groundbreaking innovations inevitably brings hurdles and periods of uncertainty. In much the same way, while the path ahead for string theory is uncertain, its potential as a unifying theory of physics keeps it at the forefront of scientific discussion.

Though the journey continues, string theory remains one of the most tantalizing possibilities for finally understanding the universe at its deepest level. Whether or not it achieves this lofty ambition, its contributions to the field of theoretical physics will undoubtedly inspire future generations to keep questioning, keep exploring, and keep searching for that elusive “theory of everything.”

<Quantum strings in multidimensional space>

Focus Keyphrase: string theory

/2 Comments/by

Simplifying Quantum Field Theory Calculations with Python Programming

Exploring Quantum Field Theory: Simplifying Complex Calculations with Python

Quantum Field Theory (QFT) stands as a monumental framework in theoretical physics, merging classical field theory, quantum mechanics, and special relativity. It provides a comprehensive description of particle physics and has been instrumental in the development of many modern physics theories, including the Standard Model. However, the mathematical complexity involved in QFT can be daunting, often involving sophisticated calculations that are not straightforward to perform manually. As someone deeply interested in physics and quantum field theory, I have explored ways to simplify these complex calculations, leveraging my programming skills to develop accessible solutions.

The Challenge: Calculating Feynman Diagrams

Feynman diagrams are graphical representations of the mathematical expressions describing the behavior and interactions of subatomic particles in quantum field theory. These diagrams are not only a tool for visualization but also serve as the foundation for calculations within the field. The primary challenge here is simplifying the process of calculating amplitudes from these diagrams, which is essential for predicting the outcomes of particle interactions.

Solution Overview

To address this challenge, we’ll develop a Python solution that simplifies the calculation of Feynman diagrams. Python, with its rich ecosystem of scientific libraries such as NumPy and SciPy, provides a powerful platform for performing complex mathematical operations. Our solution will focus on the following steps:

  • Representing Feynman diagrams in a programmable format.
  • Automating the calculation of amplitudes for each diagram.
  • Simplifying the integration of these amplitudes over momentum space.

Step 1: Representing Feynman Diagrams

To programmatically represent Feynman diagrams, we’ll define a simple data structure that captures the components of a diagram, such as vertices and lines (representing particles).

class FeynmanDiagram:
    def __init__(self, vertices, lines):
        self.vertices = vertices
        self.lines = lines

# Example: e- e+ scattering
diagram = FeynmanDiagram(vertices=["e-", "e+", "Photon", "e-", "e+"], lines=["e-", "Photon", "e+"])
print(diagram.vertices)

Step 2: Automating Calculations

With our diagrams programmatically represented, the next step involves automating the calculation of amplitudes. This process requires applying the rules for Feynman diagrams, which translate the diagrams into mathematical expressions.

def calculate_amplitude(diagram):
    # Placeholder function for calculating diagram amplitudes
    # In practice, this would involve applying Feynman rules to the given diagram
    return "Amplitude Calculation Placeholder"

print(calculate_amplitude(diagram))

Step 3: Integrating Over Momentum Space

The final step is to integrate the calculated amplitudes over momentum space, which is crucial for obtaining physical predictions from the theory. This can be achieved by leveraging the SciPy library, which provides numerical integration capabilities.

from scipy.integrate import quad

def integrate_amplitude(amplitude, start, end):
    # This is a simplified example. The actual integration would depend on the specific form of the amplitude.
    result, _ = quad(lambda x: eval(amplitude), start, end)
    return result

# Example integration (placeholder amplitude function)
print(integrate_amplitude("x**2", 0, 1))

Conclusion

In this article, we explored a programming solution to simplify the complex calculations involved in Quantum Field Theory, specifically for calculating Feynman diagrams. Through Python, we have demonstrated a practical approach that can make these calculations more accessible. While the code snippets provided are simplified, they lay the groundwork for developing more sophisticated tools for QFT calculations. My background in artificial intelligence and machine learning, combined with a deep interest in physics, motivated me to develop this solution, demonstrating the powerful synergy between programming and theoretical physics.

For those interested in diving deeper into the intricacies of Quantum Field Theory and its computational aspects, I recommend exploring further reading and resources on the topic. The journey through QFT is a challenging but rewarding one, offering profound insights into the fundamental workings of our universe.

/0 Comments/by
Link to: Get in touch

Let’s collaborate!

Contact Me

DAVID MAIOLO

 The content on this website, including text, photographs, and any other media, is the property of David Maiolo unless otherwise noted. No part of this website may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the owner.

DISCLAIMER

The information provided on this website is for general informational purposes only. While I strive to keep the information up-to-date and correct, I make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will I be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. *This website may include links to other websites which are not under the control of David Maiolo. I have no control over the nature, content, and availability of those sites.

© 2024 David Maiolo