Exploring Modular Arithmetic: Applications in Cryptography and AI

Modular arithmetic, a cornerstone of number theory, has profound implications in various fields, including cryptography and artificial intelligence. In this article, we’ll delve into the math behind modular arithmetic and demonstrate how it can be applied in areas like data encryption and algorithm optimization. This exploration is particularly relevant given my background in AI, cloud solutions, and security at DBGM Consulting, Inc..

Understanding Modular Arithmetic

Modular arithmetic revolves around the concept of congruence. Two integers \( a \) and \( b \) are said to be congruent modulo \( n \) if their difference is divisible by \( n \). This is denoted as:

\( a \equiv b \ (\text{mod} \ n) \)

For instance, \( 17 \equiv 2 \ (\text{mod} \ 5) \) because \( 17 – 2 = 15 \), and 15 is divisible by 5.

This concept can be extended to operations such as addition, subtraction, and multiplication. For example:

\( (a + b) \ \text{mod} \ n = (a \ \text{mod} \ n + b \ \text{mod} \ n) \ \text{mod} \ n \)
\( (a – b) \ \text{mod} \ n = (a \ \text{mod} \ n – b \ \text{mod} \ n) \ \text{mod} \ n \)
\( (a \cdot b) \ \text{mod} \ n = (a \ \text{mod} \ n \cdot b \ \text{mod} \ n) \ \text{mod} \ n \)

Applications in Cryptography

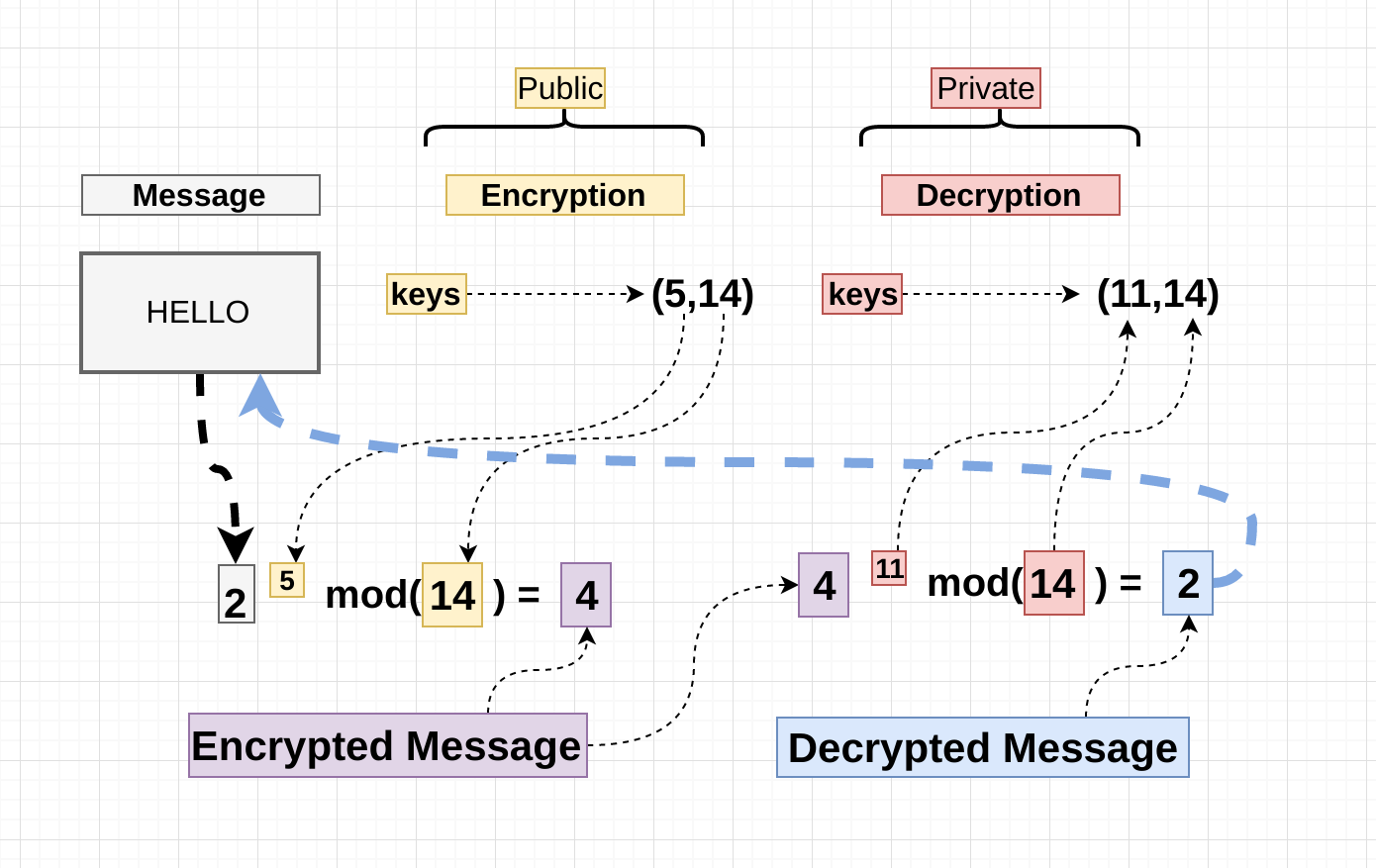
One of the most significant applications of modular arithmetic is in cryptography. Cryptographic algorithms often rely on the difficulty of solving problems like the discrete logarithm problem or the integer factorization problem within modular arithmetic. A notable example is the RSA encryption algorithm.

In RSA, the security of encrypted messages relies on the difficulty of factoring the product of two large prime numbers. The public key is generated using modular exponentiation:

\( c = m^e \ (\text{mod} \ n) \)

Here, \( m \) is the plaintext message, \( e \) is the encryption exponent, \( n \) is the product of two primes, and \( c \) is the ciphertext.

The RSA Algorithm

Choose two distinct prime numbers \( p \) and \( q \).
Compute \( n = p \cdot q \) and \( \phi(n) = (p – 1)(q – 1) \).
Select an integer \( e \) such that \( 1 < e < \phi(n) \) and \( \text{gcd}(e, \phi(n)) = 1 \).
Determine \( d \) as the modular multiplicative inverse of \( e \mod \phi(n) \), meaning \( e \cdot d \equiv 1 \ (\text{mod} \ \phi(n)) \).
Public key is \( (e, n) \) and private key is \( (d, n) \).
Encryption: \( c = m^e \mod n \).
Decryption: \( m = c^d \mod n \).

This process illustrates how modular arithmetic underpins the security of RSA, making it crucial for secure communications.

Enhancing AI with Modular Arithmetic

Modular arithmetic also plays a role in artificial intelligence, especially in optimizing algorithms and managing computational challenges. For instance, modular arithmetic can enhance the efficiency of hash functions used in data structures like hash tables, ensuring faster data retrieval and storage.

Moreover, in machine learning, modular arithmetic can be employed in stochastic gradient descent algorithms. By leveraging modulus operations, we can manage large integer computations more efficiently, reducing computational load and improving the scalability of machine learning models.

Practical Example: Custom CCD Control Board Development

In a project I worked on with my amateur astronomer friends in upstate New York, we developed a custom CCD control board for a Kodak sensor. This involved intricate timing and signal processing, which was made more efficient by employing modular arithmetic in our algorithms to handle cyclic data patterns.

Conclusion

Modular arithmetic is a fundamental mathematical concept with far-reaching implications in cryptography and artificial intelligence. Its ability to simplify complex problems and enhance computational efficiency makes it an invaluable tool in both theoretical and applied mathematics. As we continue to explore its applications, modular arithmetic will undoubtedly remain a cornerstone of modern technological advancements, from securing data to optimizing AI algorithms.

For further reading on related topics, check out my previous articles on Understanding Prime Factorization and Mitigating AI Hallucinations in Community College Classrooms.

Focus Keyphrase: modular arithmetic applications

Unlocking the Mysteries of Prime Factorization in Number Theory

In the realm of mathematics, Number Theory stands as one of the most intriguing and foundational disciplines, with prime factorization representing a cornerstone concept within this field. This article will explore the mathematical intricacies of prime factorization and illuminate its applications beyond theoretical mathematics, particularly in the areas of cybersecurity within artificial intelligence and cloud solutions, domains where I, David Maiolo, frequently apply advanced mathematical concepts to enhance security measures and optimize processes.

Understanding Prime Factorization

Prime factorization, at its core, involves decomposing a number into a product of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The beauty of prime numbers lies in their fundamental role as the “building blocks” of the natural numbers.

The mathematical expression for prime factorization can be represented as:

\[N = p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_n^{e_n}\]

where \(N\) is the natural number being factorized, \(p_1, p_2, \ldots, p_n\) are the prime factors of \(N\), and \(e_1, e_2, \ldots, e_n\) are their respective exponents indicating the number of times each prime factor is used in the product.

Applications in Cybersecurity

The concept of prime factorization plays a pivotal role in the field of cybersecurity, specifically in the development and application of cryptographic algorithms. Encryption methods, such as RSA (Rivest–Shamir–Adleman), fundamentally rely on the difficulty of factoring large prime numbers. The security of RSA encryption is underpinned by the principle that while it is relatively easy to multiply two large prime numbers, factoring their product back into the original primes is computationally challenging, especially as the size of the numbers increases.

Enhancing AI and Cloud Solutions

In my work through DBGM Consulting, Inc., applying advanced number theory concepts like prime factorization allows for the fortification of AI and cloud-based systems against cyber threats. By integrating robust encryption protocols rooted in number theory, we can ensure the security and integrity of data, a critical concern in both AI development and cloud migrations.

Linking Prime Factorization to Previous Articles

Prime factorization’s relevance extends beyond cybersecurity into the broader mathematical foundations supporting advancements in AI and machine learning, topics discussed in previous articles on my blog. For instance, understanding the role of calculus in neural networks or exploring the future of structured prediction in machine learning necessitates a grounding in basic mathematical principles, including those found in number theory. Prime factorization, with its far-reaching applications, exemplifies the deep interconnectedness of mathematics and modern technological innovations.

Conclusion

The exploration of prime factorization within number theory reveals a world where mathematics serves as the backbone of technological advancements, particularly in securing digital infrastructures. As we push the boundaries of what is possible with artificial intelligence and cloud computing, grounding our innovations in solid mathematical concepts like prime factorization ensures not only their efficiency but also their resilience against evolving cyber threats.

429 for Popular RSA encryption library

In essence, prime factorization embodies the harmony between theoretical mathematics and practical application, a theme that resonates throughout my endeavors in AI, cybersecurity, and cloud solutions at DBGM Consulting, Inc.

Focus Keyphrase:

Prime Factorization in Number Theory

Tag Archive for: RSA encryption