Tag Archive for: probability theory

Unveiling the Mathematical Foundations of Large Language Models in AI

The Mathematical Underpinnings of Large Language Models in Machine Learning

As we continue our exploration into the depths of machine learning, it becomes increasingly clear that the success of large language models (LLMs) hinges on a robust foundation in mathematical principles. From the algorithms that drive understanding and generation of text to the optimization techniques that fine-tune performance, mathematics forms the backbone of these advanced AI systems.

Understanding the Core: Algebra and Probability in LLMs

At the heart of every large language model, such as GPT (Generative Pre-trained Transformer) and BERT (Bidirectional Encoder Representations from Transformers), lies linear algebra combined with probability theory. These models learn to predict the probability of a word or sequence of words occurring in a sentence, an application deeply rooted in statistics.

  • Linear Algebra: Essential for managing the vast matrices that represent the embeddings and transformations within neural networks, enabling operations that capture patterns in data.
  • Probability: Provides the backbone for understanding and predicting language through Markov models and softmax functions, crucial for generating coherent and contextually relevant text.

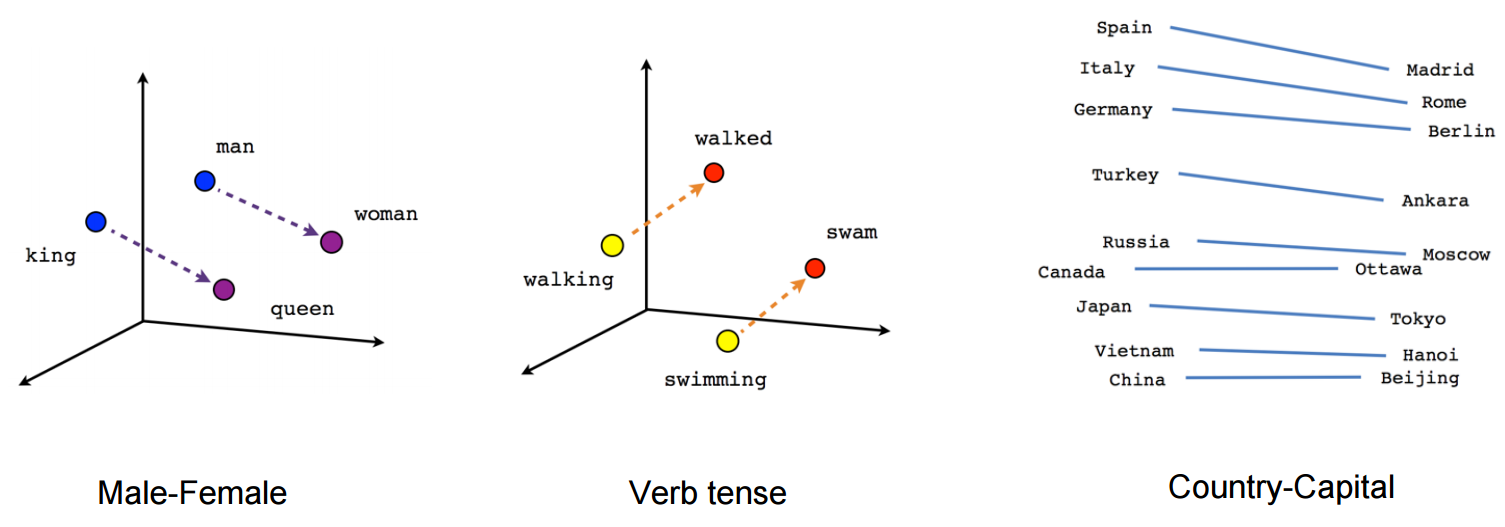
Deep Dive: Vector Spaces and Embeddings

Vector spaces, a concept from linear algebra, are paramount in translating words into numerical representations. These embeddings capture semantic relationships, such as similarity and analogy, enabling LLMs to process text in a mathematically tractable way.

<Word embeddings vector space>

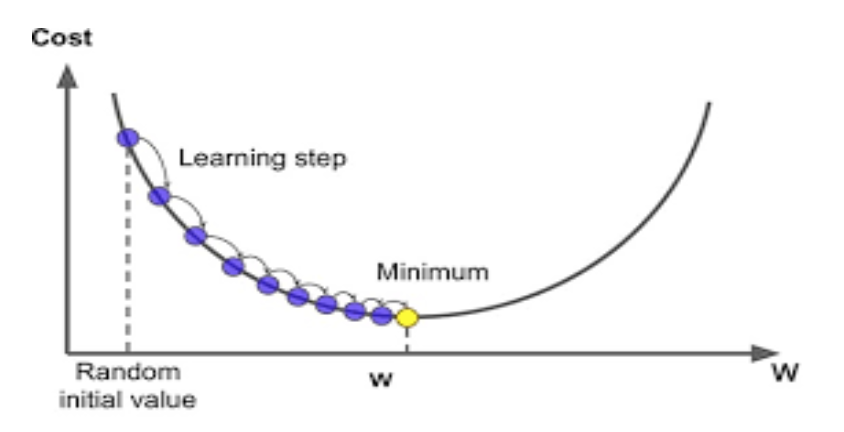
Optimization: The role of Calculus in Training AI Models

Training an LLM is fundamentally an optimization problem. Techniques from calculus, specifically gradient descent and its variants, are employed to minimize the difference between the model’s predictions and actual outcomes. This process iteratively adjusts the model’s parameters (weights) to improve its performance on a given task.

<Gradient descent in machine learning>

Dimensionality Reduction: Enhancing Model Efficiency

In previous discussions, we delved into dimensionality reduction’s role in LLMs. Techniques like PCA (Principal Component Analysis) and t-SNE (t-distributed Stochastic Neighbor Embedding) are instrumental in compressing information while preserving the essence of data, leading to more efficient computation and potentially uncovering hidden patterns within the language.

Case Study: Maximizing Cloud Efficiency Through Mathematical Optimization

My work in cloud solutions, detailed at DBGM Consulting, demonstrates the practical application of these mathematical principles. By leveraging calculus-based resource optimization techniques, we can achieve peak efficiency in cloud deployments, a concept I explored in a previous article on maximizing cloud efficiency through calculus.

Looking Ahead: The Future of LLMs and Mathematical Foundations

The future of large language models is inextricably linked to advances in our understanding and application of mathematical concepts. As we push the boundaries of what’s possible with AI, interdisciplinary research in mathematics will be critical in addressing the challenges of scalability, efficiency, and ethical AI development.

Continuous Learning and Adaptation

The field of machine learning is dynamic, necessitating a commitment to continuous learning. Keeping abreast of new mathematical techniques and understanding their application within AI will be crucial for anyone in the field, mirroring my own journey from a foundation in AI at Harvard to practical implementations in consulting.

<Abstract concept machine learning algorithms>

Conclusion

In sum, the journey of expanding the capabilities of large language models is grounded in mathematics. From algebra and calculus to probability and optimization, these foundational elements not only power current innovations but will also light the way forward. As we chart the future of AI, embracing the complexity and beauty of mathematics will be essential in unlocking the full potential of machine learning technologies.

Focus Keyphrase: Mathematical foundations of machine learning

/2 Comments/by

How Bayesian Inference Revolutionizes AI: Unveiling Probability’s Power

The Beauty of Bayesian Inference in AI: A Deep Dive into Probability Theory

Probability theory, a fundamental pillar of mathematics, has long intrigued scholars and practitioners alike with its ability to predict outcomes and help us understand the likelihood of events. Within this broad field, Bayesian inference stands out as a particularly compelling concept, offering profound implications for artificial intelligence (AI) and machine learning (ML). As someone who has navigated through the complexities of AI and machine learning, both academically at Harvard and through practical applications at my firm, DBGM Consulting, Inc., I’ve leveraged Bayesian methods to refine algorithms and enhance decision-making processes in AI models.

Understanding Bayesian Inference

At its core, Bayesian inference is a method of statistical inference in which Bayes’ theorem is used to update the probability for a hypothesis as more evidence or information becomes available. It is expressed mathematically as:

Posterior Probability = (Likelihood x Prior Probability) / Evidence

This formula essentially allows us to adjust our hypotheses in light of new data, making it an invaluable tool in the development of adaptive AI systems.

The Mathematics Behind Bayesian Inference

The beauty of Bayesian inference lies in its mathematical foundation. The formula can be decomposed as follows:

  • Prior Probability (P(H)): The initial probability of the hypothesis before new data is collected.
  • Likelihood (P(E|H)): The probability of observing the evidence given that the hypothesis is true.
  • Evidence (P(E)): The probability of the evidence under all possible hypotheses.
  • Posterior Probability (P(H|E)): The probability that the hypothesis is true given the observed evidence.

This framework provides a systematic way to update our beliefs in the face of uncertainty, a fundamental aspect of learning and decision-making in AI.

Application in AI and Machine Learning

Incorporating Bayesian inference into AI and machine learning models offers several advantages. It allows for more robust predictions, handles missing data efficiently, and provides a way to incorporate prior knowledge into models. My work with AI, particularly in developing machine learning algorithms for self-driving robots and cloud solutions, has benefited immensely from these principles. Bayesian methods have facilitated more nuanced and adaptable AI systems that can better predict and interact with their environments.

Bayesian Networks

One application worth mentioning is Bayesian networks, a type of probabilistic graphical model that uses Bayesian inference for probability computations. These networks are instrumental in dealing with complex systems where interactions between elements play a crucial role, such as in predictive analytics for supply chain optimization or in diagnosing systems within cloud infrastructure.

Linking Probability Theory to Broader Topics in AI

The concept of Bayesian inference ties back seamlessly to the broader discussions we’ve had on my blog around the role of calculus in neural networks, the pragmatic evolution of deep learning, and understanding algorithms like Gradient Descent. Each of these topics, from the Monty Hall Problem’s insights into AI and ML to the intricate discussions around cognitive computing, benefits from a deep understanding of probability theory. It underscores the essential nature of probability in refining algorithms and enhancing the decision-making capabilities of AI systems.

The Future of Bayesian Inference in AI

As we march towards a future enriched with AI, the role of Bayesian inference only grows in stature. Its ability to meld prior knowledge with new information provides a powerful framework for developing AI that more closely mirrors human learning and decision-making processes. The prospective advancements in AI, from more personalized AI assistants to autonomous vehicles navigating complex environments, will continue to be shaped by the principles of Bayesian inference.

In conclusion, embracing Bayesian inference within the realm of AI presents an exciting frontier for enhancing machine learning models and artificial intelligence systems. By leveraging this statistical method, we can make strides in creating AI that not only learns but adapts with an understanding eerily reminiscent of human cognition. The journey through probability theory, particularly through the lens of Bayesian inference, continues to reveal a treasure trove of insights for those willing to delve into its depths.

Focus Keyphrase: Bayesian inference in AI

/2 Comments/by

Understanding the Monty Hall Problem: Insights for AI and ML

Demystifying the Monty Hall Problem: A Probability Theory Perspective

As someone deeply entrenched in the realms of Artificial Intelligence (AI) and Machine Learning (ML), I often revisit foundational mathematical concepts that underpin these technologies. Today, I’d like to take you through an intriguing puzzle from probability theory known as the Monty Hall problem. This seemingly simple problem offers profound insights not only into the world of mathematics but also into decision-making processes in AI.

Understanding the Monty Hall Problem

The Monty Hall problem is based on a game show scenario where a contestant is presented with three doors. Behind one door is a coveted prize, while the other two conceal goats. The contestant selects a door, and then the host, who knows what’s behind each door, opens one of the remaining doors to reveal a goat. The contestant is then offered a chance to switch their choice to the other unopened door. Should they switch?

Intuitively, one might argue that it doesn’t matter; the odds should be 50/50. However, probability theory tells us otherwise. The probability of winning by switching is actually 2/3, while staying with the original choice gives a probability of 1/3 of finding the car.

The Math Behind It

The initial choice of the door has a 1/3 chance of being the prize door and a 2/3 chance of being a goat door. When the host opens another door to reveal a goat, the 2/3 probability of the initial choice being incorrect doesn’t just vanish; instead, it transfers to the remaining unopened door. Thus, switching doors leverages the initial probability to the contestant’s advantage.

Formally, this can be represented as:

  • P(Win | Switch) = P(Goat initially chosen) × P(Host reveals goat | Goat initially chosen) × P(Switch to Car)
  • Which simplifies to: 2/3
  • P(Win | Stay) = P(Car initially chosen) × P(Host reveals goat | Car initially chosen) × P(Stay)
  • Which simplifies to: 1/3

These probabilities provide a stark illustration of how our intuitions about chance and strategy can sometimes mislead us, a lesson that’s crucial in the development and tuning of AI algorithms.

Application in AI and Machine Learning

In AI, decision-making often involves evaluating probabilities and making predictions based on incomplete information. The Monty Hall problem serves as a metaphor for the importance of revising probabilities when new information is available. In Bayesian updating, a concept closely related to structured prediction in machine learning, prior probabilities are updated in the light of new, relevant data – akin to the contestant recalculating their odds after the host reveals a goat.

This principle is pivotal in scenarios such as sensor fusion in robotics, where multiple data sources provide overlapping information about the environment, and decisions must be continuously updated as new data comes in.

Revisiting Previous Discussions

In my exploration of topics like Structured Prediction in Machine Learning and Bayesian Networks in AI, the underlying theme of leveraging probability to improve decision-making and predictions has been recurrent. The Monty Hall problem is a testament to the counterintuitive nature of probability theory, which continually underscores the development of predictive models and analytical tools in AI.

Conclusion

As we delve into AI and ML’s mathematical foundations, revisiting problems like Monty Hall reinvigorates our appreciation for probability theory’s elegance and its practical implications. By challenging our intuitions and encouraging us to look beyond the surface, probability theory not only shapes the algorithms of tomorrow but also refines our decision-making strategies in the complex, uncertain world of AI.

For AI professionals and enthusiasts, the Monty Hall problem is a reminder of the critical role that mathematical reasoning plays in driving innovations and navigating the challenges of machine learning and artificial intelligence.

Reflection

Tackling such problems enhances not only our technical expertise but also our philosophical understanding of uncertainty and decision-making – a duality that permeates my work in AI, photography, and beyond.

Monty Hall Problem Illustration
Bayesian Network example

As we move forward, let’s continue to find inspiration in the intersection of mathematics, technology, and the broader questions of life’s uncertain choices.


/2 Comments/by
Link to: Get in touch

Let’s collaborate!

Contact Me

DAVID MAIOLO

 The content on this website, including text, photographs, and any other media, is the property of David Maiolo unless otherwise noted. No part of this website may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the owner.

DISCLAIMER

The information provided on this website is for general informational purposes only. While I strive to keep the information up-to-date and correct, I make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will I be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. *This website may include links to other websites which are not under the control of David Maiolo. I have no control over the nature, content, and availability of those sites.

© 2024 David Maiolo