Understanding Prime Factorization: The Building Blocks of Number Theory
Number Theory is one of the most fascinating branches of mathematics, often considered the ‘purest’ form of mathematical study. At its core lies the concept of prime numbers and their role in prime factorization. This mathematical technique has intrigued mathematicians for centuries and finds significant application in various fields, including computer science, cryptography, and even artificial intelligence.
Let’s delve into the concept of prime factorization and explore not just its mathematical beauty but also its practical implications.
What is Prime Factorization?
Prime factorization is the process of decomposing a composite number into a product of its prime factors. In simple terms, it involves breaking down a number until all the remaining factors are prime numbers. For instance, the number 60 can be factorized as:
\[ 60 = 2^2 \times 3 \times 5 \]
In this example, 2, 3, and 5 are prime numbers, and 60 is expressed as their product. The fundamental theorem of arithmetic assures us that this factorization is unique for any given number.
< >
>
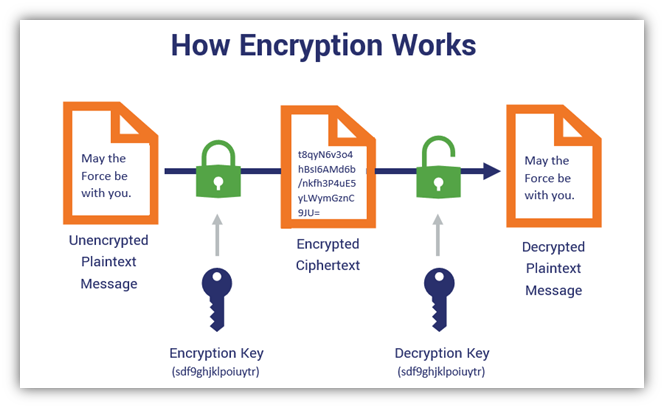
Applications in Cryptography
The concept of prime factorization is crucial in modern cryptography, particularly in public-key cryptographic systems such as RSA (Rivest-Shamir-Adleman). RSA encryption relies on the computational difficulty of factoring large composite numbers. While it’s easy to multiply two large primes to get a composite number, reversing the process (factorizing the composite number) is computationally intensive and forms the backbone of RSA’s security.
Here’s the basic idea of how RSA encryption utilizes prime factorization:
- Select two large prime numbers, \( p \) and \( q \)
- Compute their product, \( n = p \times q \)
- Choose an encryption key \( e \) that is coprime with \((p-1)(q-1)\)
- Compute the decryption key \( d \) such that \( e \cdot d \equiv 1 \mod (p-1)(q-1) \)
Because of the difficulty of factorizing \( n \), an eavesdropper cannot easily derive \( p \) and \( q \) and, by extension, cannot decrypt the message.
<
>
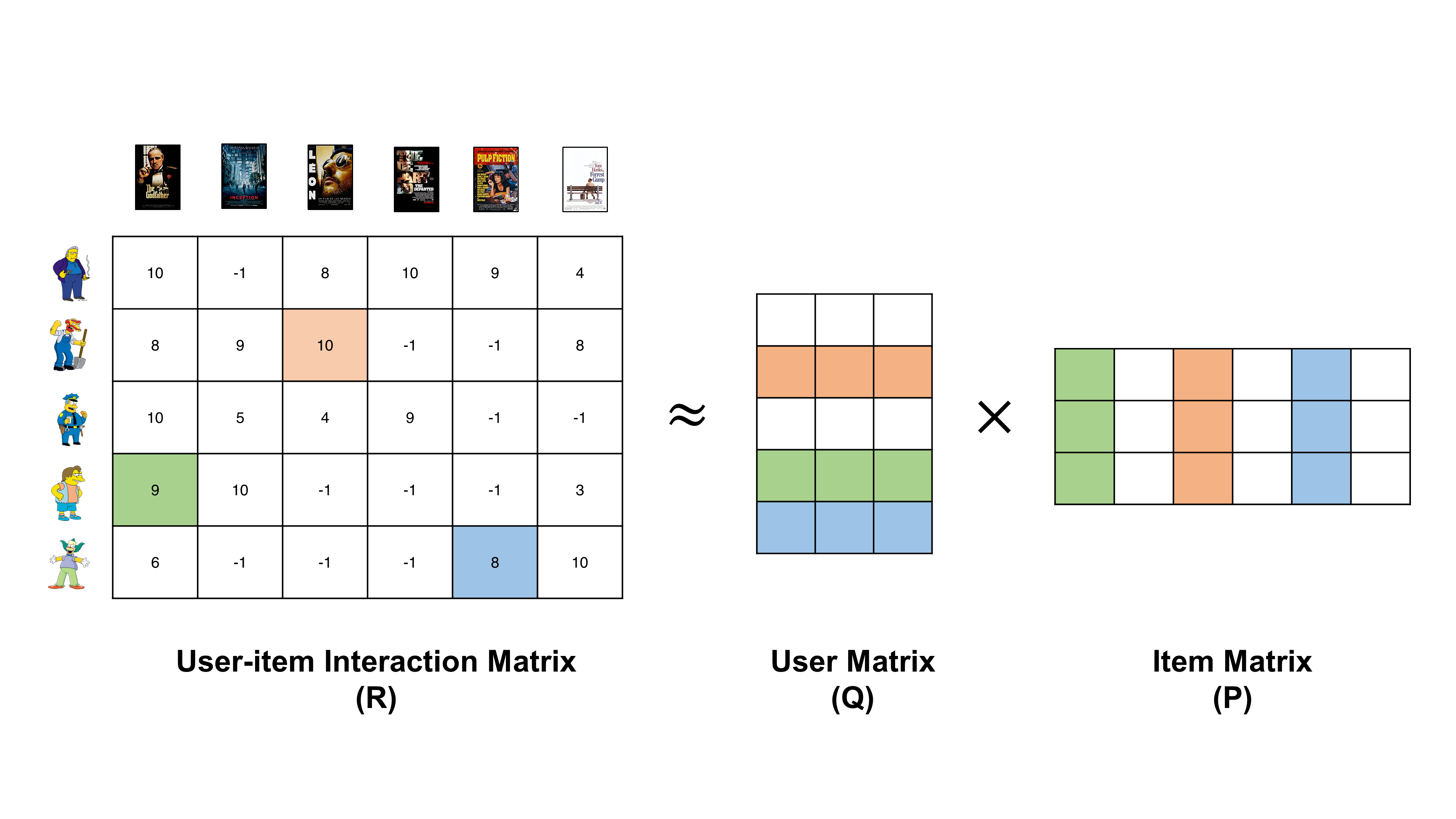
Prime Factorization and Machine Learning
While prime factorization may seem rooted in pure mathematics, it has real-world applications in AI and machine learning as well. When developing new algorithms or neural networks, understanding the foundational mathematics can provide insights into more efficient computations.
For instance, matrix factorization is a popular technique in recommender systems, where large datasets are decomposed into simpler matrices to predict user preferences. Similarly, understanding the principles of prime factorization can aid in optimizing algorithms for big data processing.
< >
>
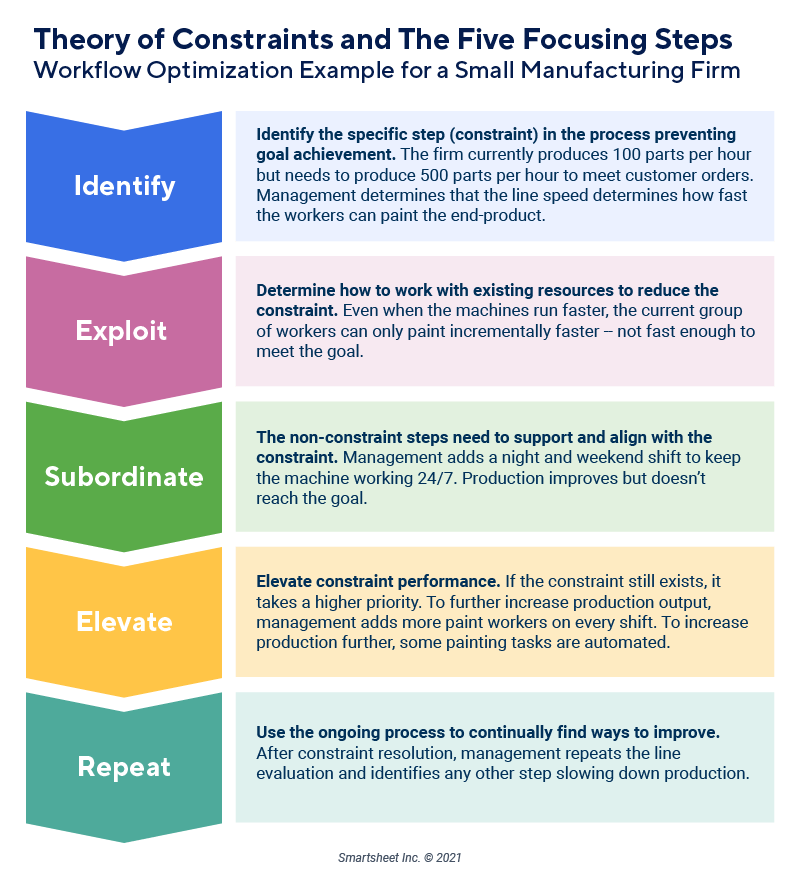
Practical Example: Process Automation
In my consulting work at DBGM Consulting, Inc., we frequently engage in process automation projects where recognizing patterns and breaking them down into simpler components is essential. Prime factorization serves as a perfect analogy for our work in breaking down complex tasks into manageable, automatable parts.
For example, consider a workflow optimization project in a large enterprise. By deconstructing the workflow into prime components such as data collection, processing, and reporting, we can create specialized AI models for each component. This modular approach ensures that each part is optimized, leading to an efficient overall system.
< >
>
Conclusion
Prime factorization is not just a theoretical exercise but a powerful tool with practical applications in various domains, from cryptography to machine learning and process automation. Its unique properties and the difficulty of factoring large numbers underpin the security of modern encryption algorithms and contribute to the efficiency of various computational tasks. Understanding and leveraging these foundational principles allows us to solve more complex problems in innovative ways.
As I’ve discussed in previous articles, particularly in the realm of Number Theory, fundamental mathematical concepts often find surprising and valuable applications in our modern technological landscape. Exploring these intersections can offer new perspectives and solutions to real-world problems.
Focus Keyphrase: Prime Factorization