Tag Archive for: Post-Quantum Cryptography

The Intriguing Role of Regex in Prime Number Detection and AI

The Curious Case of Regular Expressions and Prime Numbers

Prime numbers have fascinated mathematicians for centuries, holding a central place in the foundation of number theory and cryptography. From my background in artificial intelligence and computational systems, I tend to look for practical methods and efficient algorithms to address challenges. However, encountering a seemingly “magical” method to identify prime numbers through purely symbolic means, like regular expressions (or regex), piqued my skeptic yet intrigued mind.

Demystifying the Regex-based Prime Test

The use of regex to determine whether a number is prime may appear esoteric at first. After all, regular expressions are typically used to match strings and patterns in text, not perform arithmetic. The trick lies in how you interpret the input and the clever use of regex syntax and constructs.

This particular prime-checking regex query operates in Python, a language widely used in AI and data science, and involves transforming a number into a specific string form—a tally of ones, for example. Simply put, this process interprets numbers as strings of repeated characters like “1”. It then attempts to break this string down using regular expression patterns to see if it can exactly divide into subgroups, which corresponds to finding whether a number has any divisors other than one and itself. If it does, it is composite; if not, it is prime.

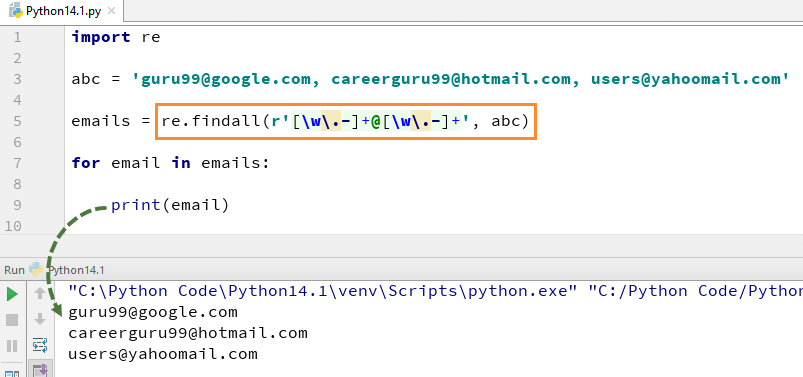Breaking Down the Regex Symbols

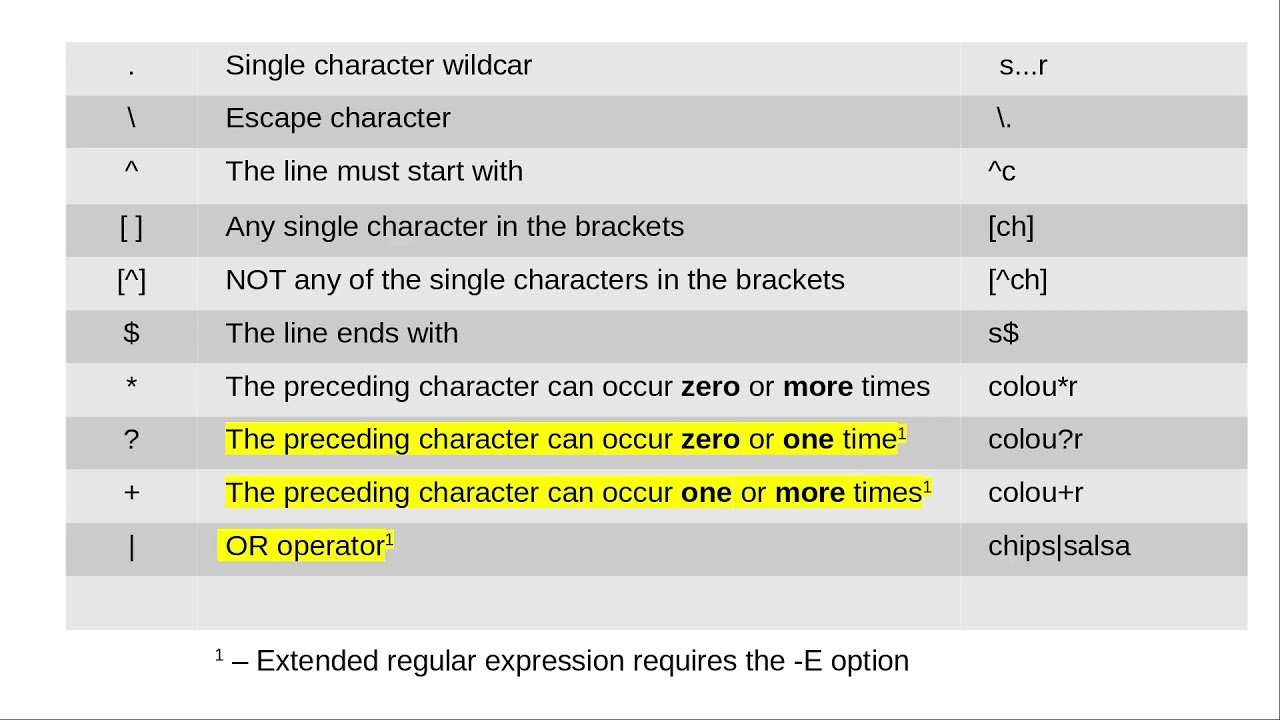
For those unfamiliar with regex syntax, the following can make the prime detection process less “spooky” (though perfect for a Halloween-themed discussion):

A dot . represents any character (a wildcard).
A plus + means “one or more” of the previous element.
The question mark ? makes the matching process “lazy”, stopping at the shortest possible string that matches the regex pattern.
Up arrows ^ and dollar signs $ indicate the start and end of a string, ensuring the entire sequence is examined.
The forward slash notation \1 calls back to a previous match, allowing the system to reuse prior captured groups—key in testing factors for the number in question.

By leveraging these symbols, regex can efficiently decompose each string of ones (whether it’s “11”, “111”, “1111”, etc.), and check how many ways the string can be evenly rerun back against itself. When no such division exists, the original number is prime.

A Surprisingly Efficient Algorithm?

One might assume that this method wouldn’t scale well for larger numbers due to the inefficiency of regex at such a task. However, optimizing the string breakdown process—such as using lazy matching—enables this algorithm to avoid some performance hits. It’s an interesting contrast to traditional Sieve of Eratosthenes approaches for prime detection. While regex isn’t typically designed for numerical computation, this clever use shows the linguistic flexibility programming languages like Python offer.

As a former Microsoft Solutions Architect specializing in cloud migration, I’ve often dealt with automation and optimization techniques. Here, Python’s built-in re library handles the brute force nature of regex effectively, which I compare to the optimizations I’ve worked on within AI models for process efficiency and computational scaling.

Regular Expressions in the Broader Tech Ecosystem

Aside from mathematical curiosities like prime testing, regex plays an important role in modern computing, especially in information retrieval systems. In previous work on AI search models, for instance, regex patterns are used to streamline database queries or identify information patterns within massive datasets. When scaling or migrating these solutions to the cloud, regex becomes part of the toolkit to ensure data is cleanly parsed, matched, or processed for machine learning models.

It All Goes Back to Probability

For readers familiar with my earlier articles on math and probability theory, tying these subjects back to regex patterns might seem unexpected. But probability theory and prime numbers share fundamental connections, especially in cryptography and number theory, where prime distribution characterizes randomness.

While regex might open a symbolic window into prime numbers, it raises a fundamental question: Can symbolic reasoning and pattern-matching methods replace traditional number theory methods in advanced AI or cryptographic functions? The answer, as always, remains nuanced. However, blending computational models like regex with AI frameworks already shows promise in enhancing algorithmic capabilities, such as in machine learning case studies I’ve worked on, where pattern recognition significantly accelerates problem-solving.

Conclusion

Regular expressions may not be the final frontier in prime number research, nor are they likely to replace more optimized algorithmic efficiency tools like the Sieve of Eratosthenes for large-scale computations. But as this clever symbolic solution demonstrates, the lines between symbolic manipulation and numerical computation continue to blur. And in the realm of artificial intelligence, where pattern recognition reigns supreme, methods like regex may prove unexpectedly useful when solving unique computational challenges.

Straddling both the realms of programming and number theory, regex offers us yet another glimpse into the interconnectivity of languages—whether spoken, mathematical, or computational. It’s a great reminder of how diverse techniques can emerge from seemingly unrelated fields, much in the same way as cosmic events can affect technological advances.

Focus Keyphrase: regex prime number detection

November 15, 2024/2 Comments/by David Maiolo

Artificial Intelligence (AI)

Exploring Modular Arithmetic Applications in Cryptography and AI

Exploring Modular Arithmetic: Applications in Cryptography and AI

Modular arithmetic, a cornerstone of number theory, has profound implications in various fields, including cryptography and artificial intelligence. In this article, we’ll delve into the math behind modular arithmetic and demonstrate how it can be applied in areas like data encryption and algorithm optimization. This exploration is particularly relevant given my background in AI, cloud solutions, and security at DBGM Consulting, Inc..

Understanding Modular Arithmetic

Modular arithmetic revolves around the concept of congruence. Two integers $ a $ and $ b $ are said to be congruent modulo $ n $ if their difference is divisible by $ n $. This is denoted as:

$ a \equiv b \ (\text{mod} \ n) $

For instance, $ 17 \equiv 2 \ (\text{mod} \ 5) $ because $ 17 – 2 = 15 $, and 15 is divisible by 5.

This concept can be extended to operations such as addition, subtraction, and multiplication. For example:

$ (a + b) \ \text{mod} \ n = (a \ \text{mod} \ n + b \ \text{mod} \ n) \ \text{mod} \ n $
$ (a – b) \ \text{mod} \ n = (a \ \text{mod} \ n – b \ \text{mod} \ n) \ \text{mod} \ n $
$ (a \cdot b) \ \text{mod} \ n = (a \ \text{mod} \ n \cdot b \ \text{mod} \ n) \ \text{mod} \ n $

Applications in Cryptography

One of the most significant applications of modular arithmetic is in cryptography. Cryptographic algorithms often rely on the difficulty of solving problems like the discrete logarithm problem or the integer factorization problem within modular arithmetic. A notable example is the RSA encryption algorithm.

In RSA, the security of encrypted messages relies on the difficulty of factoring the product of two large prime numbers. The public key is generated using modular exponentiation:

$ c = m^e \ (\text{mod} \ n) $

Here, $ m $ is the plaintext message, $ e $ is the encryption exponent, $ n $ is the product of two primes, and $ c $ is the ciphertext.

The RSA Algorithm

Choose two distinct prime numbers $ p $ and $ q $.
Compute $ n = p \cdot q $ and $ \phi(n) = (p – 1)(q – 1) $.
Select an integer $ e $ such that $ 1 < e < \phi(n) $ and $ \text{gcd}(e, \phi(n)) = 1 $.
Determine $ d $ as the modular multiplicative inverse of $ e \mod \phi(n) $, meaning $ e \cdot d \equiv 1 \ (\text{mod} \ \phi(n)) $.
Public key is $ (e, n) $ and private key is $ (d, n) $.
Encryption: $ c = m^e \mod n $.
Decryption: $ m = c^d \mod n $.

This process illustrates how modular arithmetic underpins the security of RSA, making it crucial for secure communications.

Enhancing AI with Modular Arithmetic

Modular arithmetic also plays a role in artificial intelligence, especially in optimizing algorithms and managing computational challenges. For instance, modular arithmetic can enhance the efficiency of hash functions used in data structures like hash tables, ensuring faster data retrieval and storage.

Moreover, in machine learning, modular arithmetic can be employed in stochastic gradient descent algorithms. By leveraging modulus operations, we can manage large integer computations more efficiently, reducing computational load and improving the scalability of machine learning models.

Practical Example: Custom CCD Control Board Development

In a project I worked on with my amateur astronomer friends in upstate New York, we developed a custom CCD control board for a Kodak sensor. This involved intricate timing and signal processing, which was made more efficient by employing modular arithmetic in our algorithms to handle cyclic data patterns.

Conclusion

Modular arithmetic is a fundamental mathematical concept with far-reaching implications in cryptography and artificial intelligence. Its ability to simplify complex problems and enhance computational efficiency makes it an invaluable tool in both theoretical and applied mathematics. As we continue to explore its applications, modular arithmetic will undoubtedly remain a cornerstone of modern technological advancements, from securing data to optimizing AI algorithms.

For further reading on related topics, check out my previous articles on Understanding Prime Factorization and Mitigating AI Hallucinations in Community College Classrooms.

Focus Keyphrase: modular arithmetic applications

May 28, 2024/2 Comments/by David Maiolo

Artificial Intelligence (AI)

Understanding Prime Factorization: Key Insights Into Number Theory, Cryptography, and AI

Understanding Prime Factorization: The Building Blocks of Number Theory

Number Theory is one of the most fascinating branches of mathematics, often considered the ‘purest’ form of mathematical study. At its core lies the concept of prime numbers and their role in prime factorization. This mathematical technique has intrigued mathematicians for centuries and finds significant application in various fields, including computer science, cryptography, and even artificial intelligence.

Let’s delve into the concept of prime factorization and explore not just its mathematical beauty but also its practical implications.

What is Prime Factorization?

Prime factorization is the process of decomposing a composite number into a product of its prime factors. In simple terms, it involves breaking down a number until all the remaining factors are prime numbers. For instance, the number 60 can be factorized as:

\[ 60 = 2^2 \times 3 \times 5 \]

In this example, 2, 3, and 5 are prime numbers, and 60 is expressed as their product. The fundamental theorem of arithmetic assures us that this factorization is unique for any given number.

Applications in Cryptography

The concept of prime factorization is crucial in modern cryptography, particularly in public-key cryptographic systems such as RSA (Rivest-Shamir-Adleman). RSA encryption relies on the computational difficulty of factoring large composite numbers. While it’s easy to multiply two large primes to get a composite number, reversing the process (factorizing the composite number) is computationally intensive and forms the backbone of RSA’s security.

Here’s the basic idea of how RSA encryption utilizes prime factorization:

Select two large prime numbers, $ p $ and $ q $
Compute their product, $ n = p \times q $
Choose an encryption key $ e $ that is coprime with $(p-1)(q-1)$
Compute the decryption key $ d $ such that $ e \cdot d \equiv 1 \mod (p-1)(q-1) $

Because of the difficulty of factorizing $ n $, an eavesdropper cannot easily derive $ p $ and $ q $ and, by extension, cannot decrypt the message.

Prime Factorization and Machine Learning

While prime factorization may seem rooted in pure mathematics, it has real-world applications in AI and machine learning as well. When developing new algorithms or neural networks, understanding the foundational mathematics can provide insights into more efficient computations.

For instance, matrix factorization is a popular technique in recommender systems, where large datasets are decomposed into simpler matrices to predict user preferences. Similarly, understanding the principles of prime factorization can aid in optimizing algorithms for big data processing.

Practical Example: Process Automation

In my consulting work at DBGM Consulting, Inc., we frequently engage in process automation projects where recognizing patterns and breaking them down into simpler components is essential. Prime factorization serves as a perfect analogy for our work in breaking down complex tasks into manageable, automatable parts.

For example, consider a workflow optimization project in a large enterprise. By deconstructing the workflow into prime components such as data collection, processing, and reporting, we can create specialized AI models for each component. This modular approach ensures that each part is optimized, leading to an efficient overall system.

Conclusion

Prime factorization is not just a theoretical exercise but a powerful tool with practical applications in various domains, from cryptography to machine learning and process automation. Its unique properties and the difficulty of factoring large numbers underpin the security of modern encryption algorithms and contribute to the efficiency of various computational tasks. Understanding and leveraging these foundational principles allows us to solve more complex problems in innovative ways.

As I’ve discussed in previous articles, particularly in the realm of Number Theory, fundamental mathematical concepts often find surprising and valuable applications in our modern technological landscape. Exploring these intersections can offer new perspectives and solutions to real-world problems.

Focus Keyphrase: Prime Factorization

May 27, 2024/2 Comments/by David Maiolo

Artificial Intelligence (AI)

Celebrating Avi Wigderson: 2023 Turing Award Laureate’s Impact on Algorithms and Randomness

The Intersection of Randomness and Algorithms: Celebrating Avi Wigderson’s Turing Award

The computing and mathematical communities have long pursued the secrets nestled within the complex relationship between randomness and predictability. It’s this intrigue that positions the recent 2023 Turing Award, given to mathematician Avi Wigderson, as not just a celebration of individual accomplishment, but a testament to the evolving dialogue between mathematics and computer science.

A Lifetime Devoted to Theoretical Computer Science

With an illustrious career at the Institute for Advanced Study, Wigderson has dedicated his professional life to unraveling the mysteries of theoretical computer science. What sets Wigderson apart is his focus not merely on solutions, but the essence of a problem’s solvability. This quest has led him to explore the realms of randomness and unpredictability in computing—a journey that highlights the essence of problem-solving itself.

Revolutionizing Algorithmic Approaches

Wigderson’s early work in the 1980s marked a pivotal shift in how algorithms were understood. He discovered that injecting randomness into algorithms could, paradoxically, lead to simpler and faster solutions. Conversely, his research also illustrated how reducing randomness could streamline the journey to an answer. These discoveries have left an indelible mark on the field, influencing everything from cryptography to cloud computing.

Redefining the P versus NP Problem

A cornerstone of Wigderson’s legacy is his contribution to the P versus NP problem, one of computer science’s most famous challenges. By integrating randomness into the equation, Wigderson not only shed light on specific proofs but also blurred the line between what constitutes an ‘easy’ and ‘hard’ problem in computational terms. His work underscores the fluid nature of problem-solving, suggesting the solutions we seek may be more a matter of perspective than inherent difficulty.

Expanding the Frontier: Beyond Computer Science

What makes Wigderson’s work truly groundbreaking is its universality. The principles of randomness and predictability he has explored do not confine themselves to computer science but extend into natural processes and the fabric of human society. From the unpredictability of stock markets to the spread of diseases, the implications of his work are both profound and pervasive.

A Legacy of Intersectionality

Wigderson’s achievements are emblematic of a broader narrative: the convergence of diverse disciplines. His recognition with both the Turing Award and the Abel Prize highlights an ever-growing acknowledgment that the future of innovation lies at the intersection of computer science and mathematics. By harnessing randomness, a concept as ancient as the universe itself, Wigderson has not only advanced our understanding but has also reminded us of the beauty in unpredictability.

In Honor of a True Pioneer

For those of us engaged in the exploration of theoretical computer science, Wigderson’s recognition serves as both an inspiration and a challenge. His journey encourages us to look beyond the binary of right answers and wrong ones, to embrace the complexity of the unknown, and to always seek the unifying threads between seemingly disparate fields. As we reflect on Wigderson’s contributions, we are reminded of the boundless potential that lies in the marriage of mathematics and computer science.

In closing, Avi Wigderson’s journey illuminates a path forward for all of us. Whether we find ourselves pondering the vastness of the cosmos, the intricacy of natural phenomena, or the elegance of a well-crafted algorithm, his work teaches us to appreciate the dance between determinism and randomness. Today, as we celebrate his achievements, we also look forward to the new horizons his work opens for future explorers in the boundless frontier of theoretical computer science and mathematics.

As we delve deeper into this fascinating intersection, we surely carry forth the torch lit by Wigderson, inspired by the vast landscape of knowledge that awaits our discovery—and the promise of unlocking yet more mysteries that string together the fabric of our universe.

Focus Keyphrase: Avi Wigderson Turing Award

April 13, 2024/2 Comments/by David Maiolo

Artificial Intelligence (AI)

Exploring the Impact of Fermat’s Little Theorem in Cryptography

Applying Fermat’s Little Theorem in Cryptography: A Number Theory Perspective

In the realm of Number Theory, an area of mathematics that has fascinated scholars for centuries, certain theorems stand out for their utility and elegance. Fermat’s Little Theorem is one such result, offering insights into the properties of prime numbers that are crucial for modern computational algorithms, including those in the field of cybersecurity and cryptography. As an individual whose expertise spans across artificial intelligence, cloud solutions, and security, I find the application of mathematical theories like Fermat’s Little Theorem particularly compelling in the way they intersect with technological advancements to enhance data security.

Understanding Fermat’s Little Theorem

Fermat’s Little Theorem states that if p is a prime number, then for any integer a such that a is not divisible by p, it is the case that a^p ≡ a (mod p). In simpler terms, when a is raised to the power of p and then divided by p, the remainder is a. This theorem plays a foundational role in understanding the behavior of numbers in modular arithmetic, an essential part of the cryptographic algorithms that protect our digital communications.

Formula Representation

To visually represent the theorem, the mathematical formula can be stated as:

a^p ≡ a (mod p)

Where:

p is a prime number.
a is an integer not divisible by p.

Application in Cryptography

The true power of Fermat’s Little Theorem unfolds in its application within the field of cryptography, particularly in the generation and encryption of digital signatures and public-key encryption schemes like RSA (Rivest-Shamir-Adleman algorithm). The RSA algorithm, for instance, relies on the properties of large prime numbers and modular exponentiation, directly incorporating concepts from Fermat’s theorem.

When creating a public RSA key, two large prime numbers are chosen and multiplied together. Fermat’s Little Theorem assists in ensuring that these numbers have properties that make the encryption secure yet feasible to compute for those with the correct key. The theorem aids in determining the modular inverse during the RSA key generation process, crucial for decrypting the received messages.

Linking Number Theory to Modern Challenges

The beauty of number theory, as demonstrated through Fermat’s Little Theorem, is its timeless relevance. As discussed in my previous articles, such as “Delving Deeper into the Mathematical Foundations of Machine Learning” and “Unlocking Complex AI Challenges with Structured Prediction and Large Language Models”, the intersection of mathematical theories with technological advancements offers a fertile ground for innovation.

In the context of cryptography, Fermat’s Little Theorem provides a mathematical foundation that supports the security mechanisms underlying the digital economy, from banking transactions to confidential communications. As we venture further into an era dominated by quantum computing and advanced AI, the principles of number theory will continue to guide the development of secure, reliable algorithms.

Conclusion

Fermat’s Little Theorem exemplifies the elegance and utility of mathematical concepts derived from number theory, transcending their origins to solve real-world problems. In the ever-evolving field of technology and cybersecurity, the theorem offers a bridge connecting the abstract world of numbers with the concrete requirements of digital security. As we continue to push the boundaries of what’s possible with AI and computing, the insights gained from number theory will undeniably play a pivotal role in shaping the future of technology.

Remember, the applications of number theory in technology exemplify the profound impact that seemingly abstract mathematical concepts can have on our world, underpinning innovations that enhance and secure our digital lives.

Focus Keyphrase: Fermat’s Little Theorem in Cryptography

March 10, 2024/2 Comments/by David Maiolo

AI Projects

SEALSQ: Leading the Way in Post-Quantum Cryptography and Semiconductor Tech in the US

“`html

SEALSQ to Pioneer Post-Quantum Cryptography with New OSAT Center in the US

As the founder of DBGM Consulting, Inc., with extensive experience in artificial intelligence and cloud solutions, the announcement by SEALSQ Corp regarding its plans to establish an Open Semiconductors Assembly and Test (OSAT) Center in the United States strikes a particular chord with me. This bold move not only emphasizes the importance of semiconductor technology in today’s digital age but also shines a spotlight on the integration of artificial intelligence and post-quantum cryptography methodologies within this sector.

The Essence of SEALSQ’s Initiative

SEALSQ’s initiative to open a US-based OSAT is no small feat; it is a calculated step towards significant advancements in the semiconductor industry. By incorporating testing services such as the wafer test and final test, along with assembly services for QFN, BGA, WLCSP, and more, SEALSQ is gearing up to redefine the standards of semiconductor technology.

Furthermore, SEALSQ is leveraging Public-Private Partnerships (PPP) for the development of Semiconductor Personalization Centers using the cutting-edge RISC-V technology. This technology allows for the local creation of chips, adhering to the highest security standards and certifications from the likes of Common Criteria and NIST.

Integrating Post-Quantum Cryptography and AI in Semiconductors

The fusion of SEALSQ semiconductors with post-quantum cryptography (PQC) and AI technology paves the way for a new era in the semiconductor field. The urgency for quantum-resistant cryptographic capabilities has never been more pronounced, especially with the looming threat of quantum computing, which could render traditional encryption methods obsolete.

PQC aims to secure communications against the computational brute force of quantum computers. The incorporation of PQC into semiconductor architectures, via methods like lattice-based and hash-based cryptography, ensures that encrypted data is safeguarded against potential quantum computing threats. When combined with the adaptive intelligence of AI, these semiconductors are not just quantum-resistant but also capable of real-time threat adaptation, optimizing performance and efficiency autonomously.

Global Push for Semiconductor Security and Supply Chain Resilience

The global landscape is currently ripe with initiatives aimed at bolstering semiconductor supply chain resilience. The US, through the International Technology Security and Innovation (ITSI) Fund established under the CHIPS Act of 2022, and the EU with its Chips Act, are investing heavily in the development and secure diversification of semiconductor networks. These steps underscore the strategic importance and national security implications tethered to semiconductor supply control.

Looking Forward

With its forward-looking statements, SEALSQ Corp illustrates a roadmap filled with optimism and challenges alike. The success of integrating PQC and AI into semiconductor architectures will not only herald a new era for digital security but also demonstrate a significant leap in technological advancement. As we venture into this promising yet uncertain future, the importance of innovations such as those proposed by SEALSQ cannot be overstated—showcasing the imperative of adapting to emerging threats while enhancing operational efficiency.

For more insightful discussions on artificial intelligence, quantum computing, and the future of technology, visit my personal blog at https://www.davidmaiolo.com.

Focus Keyphrase: Post-Quantum Cryptography

“`

February 7, 2024/0 Comments/by David Maiolo

Tag Archive for: Post-Quantum Cryptography

The Curious Case of Regular Expressions and Prime Numbers

Demystifying the Regex-based Prime Test

Breaking Down the Regex Symbols

A Surprisingly Efficient Algorithm?

Regular Expressions in the Broader Tech Ecosystem

It All Goes Back to Probability

Conclusion

Exploring Modular Arithmetic: Applications in Cryptography and AI

Understanding Modular Arithmetic

Applications in Cryptography

The RSA Algorithm

Enhancing AI with Modular Arithmetic

Practical Example: Custom CCD Control Board Development

Conclusion

Understanding Prime Factorization: The Building Blocks of Number Theory

What is Prime Factorization?

Applications in Cryptography

Prime Factorization and Machine Learning

Practical Example: Process Automation

Conclusion

The Intersection of Randomness and Algorithms: Celebrating Avi Wigderson’s Turing Award

A Lifetime Devoted to Theoretical Computer Science

Revolutionizing Algorithmic Approaches

Redefining the P versus NP Problem

Expanding the Frontier: Beyond Computer Science

A Legacy of Intersectionality

In Honor of a True Pioneer

Focus Keyphrase: Avi Wigderson Turing Award

Applying Fermat’s Little Theorem in Cryptography: A Number Theory Perspective

Understanding Fermat’s Little Theorem

Formula Representation

Application in Cryptography

Linking Number Theory to Modern Challenges

Conclusion

SEALSQ to Pioneer Post-Quantum Cryptography with New OSAT Center in the US

The Essence of SEALSQ’s Initiative

Integrating Post-Quantum Cryptography and AI in Semiconductors

Global Push for Semiconductor Security and Supply Chain Resilience

Looking Forward

Let’s collaborate!