Tag Archive for: Numerical Analysis

Exploring Numerical Analysis and Its Impact on AI and Machine Learning

Navigating Through the Roots: The Power of Numerical Analysis in Finding Solutions

From the vast universe of mathematics, there’s a specific area that bridges the gap between abstract theory and the tangible world: numerical analysis. This mathematical discipline focuses on devising algorithms to approximate solutions to complex problems – a cornerstone in the realm of computing and, more specifically, in artificial intelligence and machine learning, areas where I have dedicated much of my professional journey.

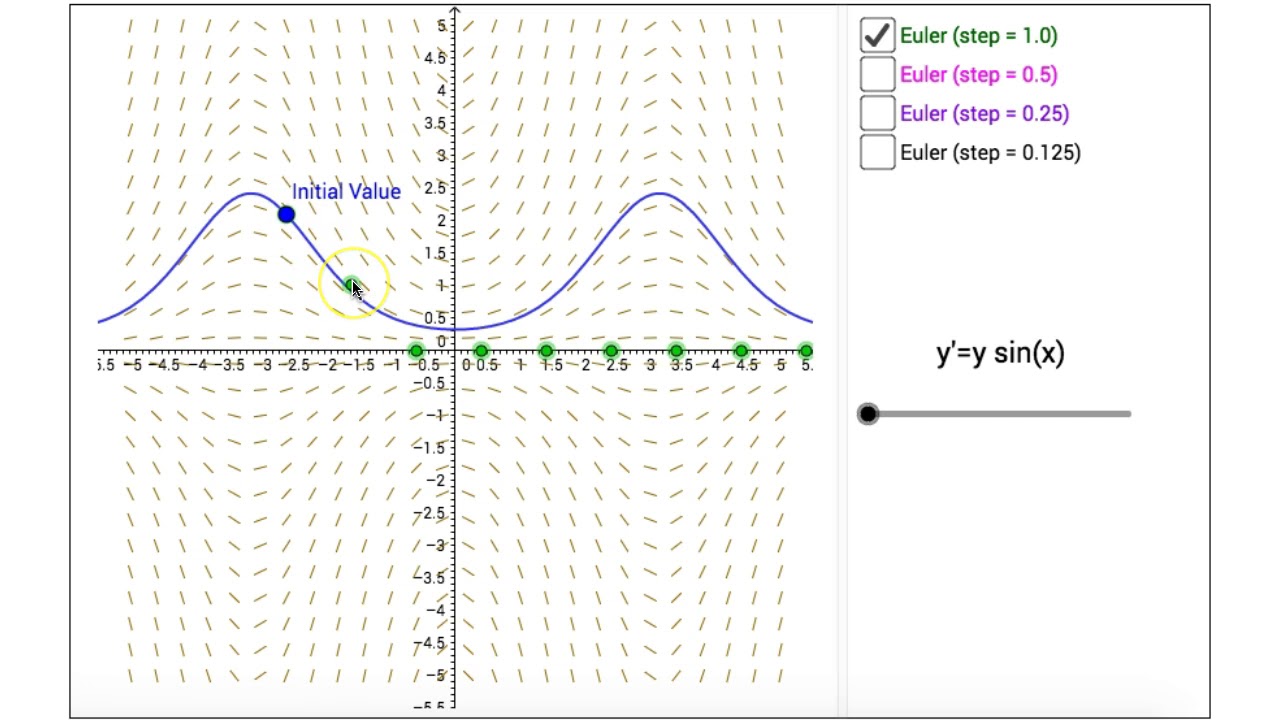
One might wonder how techniques from numerical analysis are instrumental in real-world applications. Let’s dive into a concept known as Root Finding and investigate the Bisection Method, a straightforward yet powerful approach to finding roots of functions, which exemplifies the utility of numerical methods in broader contexts such as optimizing machine learning algorithms.

Understanding the Bisection Method

The Bisection Method is a kind of bracketing method that systematically narrows down the interval within which a root of a function must lie. It operates under the premise that if a continuous function changes sign over an interval, it must cross the x-axis, and hence, a root must exist within that interval.

The algorithm is simple:

  1. Select an interval \([a, b]\) where \(f(a)\) and \(f(b)\) have opposite signs.
  2. Calculate the midpoint \(c = \frac{(a+b)}{2}\) and evaluate \(f(c)\).
  3. Determine which half-interval contains the root based on the sign of \(f(c)\) and repeat the process with the new interval.

This method exemplifies the essence of numerical analysis: starting from an initial approximation, followed by iterative refinement to converge towards a solution. The Bisection Method guarantees convergence to a root, provided the function in question is continuous on the selected interval.

Application in AI and Machine Learning

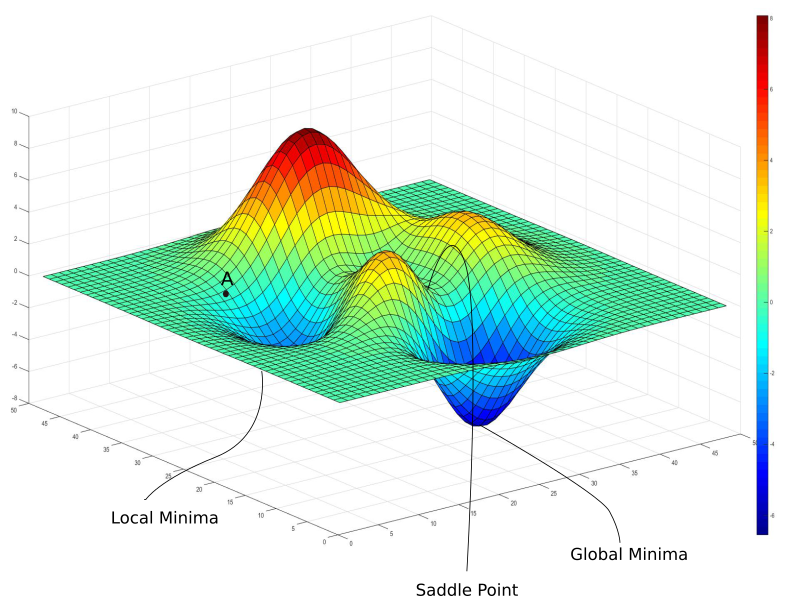
In my work with DBGM Consulting, Inc., where artificial intelligence is a cornerstone, numerical analysis plays a pivotal role, particularly in optimizing machine learning models. Models often require the tuning of hyperparameters, the process for which can be conceptualized as finding the “root” or optimal value that minimizes a loss function. Here, the Bisection Method serves as an analogy for more complex root-finding algorithms used in optimization tasks.

Imagine, for instance, optimizing a deep learning model’s learning rate. An incorrectly chosen rate could either lead the model to converge too slowly or overshoot the minimum of the loss function. By applying principles akin to the Bisection Method, one can systematically hone in on an optimal learning rate that balances convergence speed and stability.

The marvels of numerical analysis, hence, are not just confined to abstract mathematical problems but extend to solving some of the most intricate challenges in the field of artificial intelligence and beyond.

Wrap-Up

Numerical analysis is a testament to the power of mathematical tools when applied to solve real-world problems. The Bisection Method, while elementary in its formulation, is a prime example of how systemic approximation can lead to the discovery of precise solutions. In the realm of AI and machine learning, where I have spent significant portions of my career, such numerical methods underpin the advancements that drive the field forward.

As we continue to unravel complex phenomena through computing, the principles of numerical analysis will undoubtedly play a crucial role in bridging the theoretical with the practical, ushering in new innovations and solutions.

References

Deep learning model optimization graph

Bisection method convergence illustration

/0 Comments/by

Unraveling Polynomial Equations with Newton’s Method in AI and ML

Deciphering the Roots: A Numerical Analysis Perspective on Polynomial Equations

In the realm of numerical analysis, one of the most captivating quests involves finding the roots of polynomial equations. These equations, which represent myriad phenomena across disciplines, are the foundation upon which both classical and contemporary science and engineering are built. The importance of polynomial roots in computational fields, especially in Artificial Intelligence (AI) and Machine Learning (ML), cannot be overstated—they serve as key components in algorithms essential for optimization, modeling, and solving complex systems. Today, I will delve into one specific method within numerical analysis that has transformed our approach to these problems: Newton’s Method.

Understanding Newton’s Method

At its core, Newton’s Method (also known as the Newton-Raphson method) offers a powerful approach to finding successively better approximations to the roots (or zeroes) of a real-valued function. Here’s the formula that underpins this method:

Xn+1 = Xn – f(Xn)/f'(Xn)

This iterative formula suggests that if you start with an initial guess X0 that is close to the true root, you can apply this formula repeatedly to get closer and closer to the actual root of the equation. This method is particularly appealing for its simplicity and the rapid convergence it offers under favorable conditions.

Application in AI and Machine Learning

In my practice at DBGM Consulting, Inc., leveraging the power of AI and ML to solve real-world problems is paramount. Newton’s Method comes into play especially in optimization problems where we need to find the minimum or maximum of a function—which, in essence, can be transformed into a root-finding problem. For instance, in the training phase of machine learning models, optimization algorithms like gradient descent are used to minimize a cost function. Newton’s Method enhances these algorithms by providing a more efficient way to converge towards the function’s minima, thereby improving the model’s performance.

Breaking Down the Mathematics

Let’s consider a polynomial equation f(x) = x3 – 7x2 + 8x – 3 and an initial guess X0=1.5. The goal is to find a root of f(x) using Newton’s Method. The derivative of f(x), needed for our formula, is f'(x) = 3x2 – 14x + 8. Applying the Newton’s formula iteratively, we find improved approximations of the root with each step, eventually converging to a solution that, while approximate, is incredibly close to the actual root.

Challenges and Considerations

While Newton’s Method is powerful, it’s not without its challenges. The method requires a derivative, which might be difficult or impractical to obtain for complex functions. Moreover, the initial guess X0 has to be reasonably close to the true root for the method to converge. Additionally, the method does not guarantee convergence for all functions, highlighting the need for careful analysis and potentially alternative approaches in such cases.

Concluding Thoughts

The elegance of Newton’s Method in numerical analysis lies in its ability to simplify the seemingly daunting task of root-finding to iterative formula application. In AI and ML, where optimization is frequently at the heart of problem-solving, understanding and applying this method can significantly enhance algorithm efficiency and effectiveness. As we continue to push the boundaries of what these technologies can achieve, the foundations laid by numerical analysis methods like this one play an instrumental role in driving progress.

As I reflect on my journey from a Harvard University graduate focusing on information systems and AI, through my experiences at Microsoft, and into the establishment of my own firm, the unifying thread has been the constant pursuit of applying such mathematical principles to solve real-world challenges. Whether optimizing machine learning models or developing innovative cloud solutions, the essence of numerical analysis remains a cornerstone of technological advancement.

<Newton's Method Graphical Illustration>
<Optimization curves in Machine Learning>
<Real-life example of root-finding application in AI>

I invite you to explore further instances where mathematical elegance meets practical application across various fields on my blog. Let’s continue to unravel the complexity of our world, one equation at a time.

/0 Comments/by

Harnessing Numerical Methods for Superior AI Predictive Models

“`html

The Elegance of Numerical Methods in AI Predictive Models

In the realm of Artificial Intelligence and Machine Learning, precision and accuracy are paramount. It’s here that numerical analysis not only finds its application but also shines, bridging the gap between theoretical models and real-world data. As a consultant specializing in AI, I’ve witnessed firsthand the transformative power of numerical methods in predictive modeling.

Understanding Numerical Analysis

Numerical analysis is a branch of mathematics that devises, analyzes, and implements algorithms for obtaining numerical solutions to problems inherent in continuous mathematics. This discipline is the backbone of computational models, especially in areas requiring the solution of complex equations that are difficult or impossible to solve analytically.

Case Study: Solving Differential Equations

One of the most compelling examples of numerical analysis in action is in solving differential equations for predictive models. Differential equations are vital in modeling real-world processes in physics, engineering, and notably, in AI predictive models. The Role of Differential Equations in Enhancing AI Predictive Models further elucidates their importance.

Numerical Methods for Differential Equations

There are several numerical methods available for solving differential equations, such as Euler’s method, the Runge-Kutta methods, and the finite element method. Each has its advantages and specific use cases, but all serve the purpose of approximating solutions to otherwise intractable models.

Euler's method visualization

Let’s delve a bit deeper into Euler’s method, a fundamental numerical approach for solving ordinary differential equations (ODEs). It proceeds as follows:

  • Given an initial value problem \(y’=f(t,y), y(t_0)=y_0\),
  • Euler’s method approximates y at subsequent points by \(y_{n+1} = y_n + h*f(t_n, y_n)\),
  • where \(h\) is the step size and \(t_{n+1} = t_n + h\).

Although simple, Euler’s method lays the foundation for more complex algorithms and illustrates the fundamental idea of progressing step-wise to approximate solutions over a range.

Applying Numerical Methods in AI

My experience at DBGM Consulting, Inc., particularly in developing machine learning models for self-driving robots, highlighted the indispensability of numerical methods. For instance, optimizing pathfinding algorithms or sensor data interpretations invariably resorts to solving differential equations, for which numerical analysis provides the tools.

Pathfinding algorithm visualization

Numerical analysis, especially in AI, isn’t just about finding solutions—it’s also about ensuring these solutions are computationally feasible and aligned with real-world data. In essence, numerical methods help translate mathematical models into actionable intelligence, crucial for anything from process automation to predictive modeling.

Conclusion

The fusion of numerical analysis with AI and machine learning brings forth solutions that are both innovative and grounded in mathematical rigor. As someone who has navigated the intersection of technology, mathematics, and real-world application, I assert the value of numerical methods is immeasurable. They empower us to solve complex problems, optimize algorithms, and ultimately, drive forward the frontier of what’s possible in AI and beyond.

Machine learning model visualization


“`

/0 Comments/by
Link to: Get in touch

Let’s collaborate!

Contact Me

DAVID MAIOLO

 The content on this website, including text, photographs, and any other media, is the property of David Maiolo unless otherwise noted. No part of this website may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the owner.

DISCLAIMER

The information provided on this website is for general informational purposes only. While I strive to keep the information up-to-date and correct, I make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will I be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. *This website may include links to other websites which are not under the control of David Maiolo. I have no control over the nature, content, and availability of those sites.

© 2024 David Maiolo