Exploring Modular Arithmetic: Applications in Cryptography and AI

Modular arithmetic, a cornerstone of number theory, has profound implications in various fields, including cryptography and artificial intelligence. In this article, we’ll delve into the math behind modular arithmetic and demonstrate how it can be applied in areas like data encryption and algorithm optimization. This exploration is particularly relevant given my background in AI, cloud solutions, and security at DBGM Consulting, Inc..

Understanding Modular Arithmetic

Modular arithmetic revolves around the concept of congruence. Two integers \( a \) and \( b \) are said to be congruent modulo \( n \) if their difference is divisible by \( n \). This is denoted as:

\( a \equiv b \ (\text{mod} \ n) \)

For instance, \( 17 \equiv 2 \ (\text{mod} \ 5) \) because \( 17 – 2 = 15 \), and 15 is divisible by 5.

This concept can be extended to operations such as addition, subtraction, and multiplication. For example:

• \( (a + b) \ \text{mod} \ n = (a \ \text{mod} \ n + b \ \text{mod} \ n) \ \text{mod} \ n \)
• \( (a – b) \ \text{mod} \ n = (a \ \text{mod} \ n – b \ \text{mod} \ n) \ \text{mod} \ n \)
• \( (a \cdot b) \ \text{mod} \ n = (a \ \text{mod} \ n \cdot b \ \text{mod} \ n) \ \text{mod} \ n \)

Applications in Cryptography

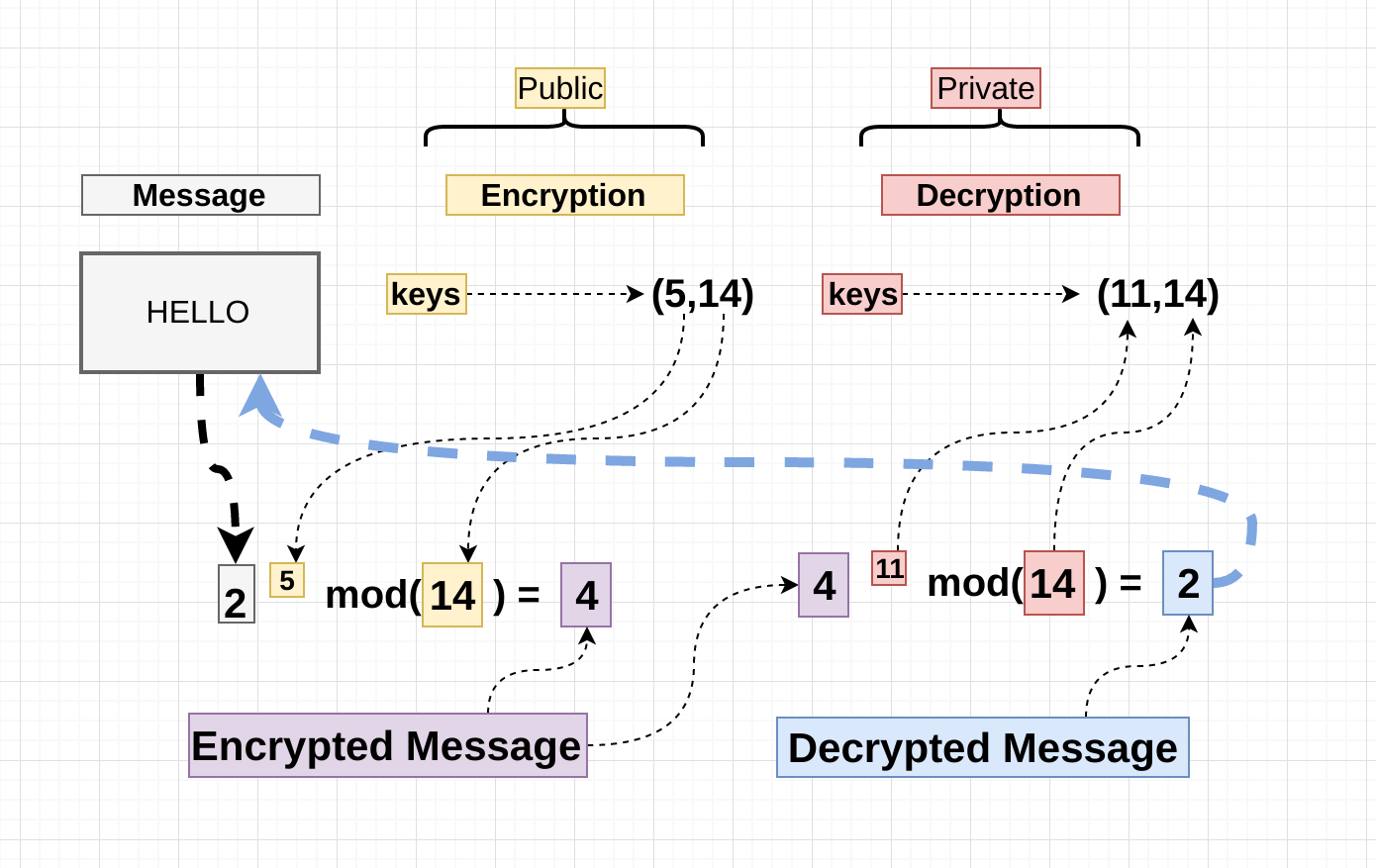
One of the most significant applications of modular arithmetic is in cryptography. Cryptographic algorithms often rely on the difficulty of solving problems like the discrete logarithm problem or the integer factorization problem within modular arithmetic. A notable example is the RSA encryption algorithm.

In RSA, the security of encrypted messages relies on the difficulty of factoring the product of two large prime numbers. The public key is generated using modular exponentiation:

\( c = m^e \ (\text{mod} \ n) \)

Here, \( m \) is the plaintext message, \( e \) is the encryption exponent, \( n \) is the product of two primes, and \( c \) is the ciphertext.

The RSA Algorithm

1. Choose two distinct prime numbers \( p \) and \( q \).
2. Compute \( n = p \cdot q \) and \( \phi(n) = (p – 1)(q – 1) \).
3. Select an integer \( e \) such that \( 1 < e < \phi(n) \) and \( \text{gcd}(e, \phi(n)) = 1 \).
4. Determine \( d \) as the modular multiplicative inverse of \( e \mod \phi(n) \), meaning \( e \cdot d \equiv 1 \ (\text{mod} \ \phi(n)) \).
5. Public key is \( (e, n) \) and private key is \( (d, n) \).
6. Encryption: \( c = m^e \mod n \).
7. Decryption: \( m = c^d \mod n \).

This process illustrates how modular arithmetic underpins the security of RSA, making it crucial for secure communications.

<>

Enhancing AI with Modular Arithmetic

Modular arithmetic also plays a role in artificial intelligence, especially in optimizing algorithms and managing computational challenges. For instance, modular arithmetic can enhance the efficiency of hash functions used in data structures like hash tables, ensuring faster data retrieval and storage.

Moreover, in machine learning, modular arithmetic can be employed in stochastic gradient descent algorithms. By leveraging modulus operations, we can manage large integer computations more efficiently, reducing computational load and improving the scalability of machine learning models.

<

>

Practical Example: Custom CCD Control Board Development

In a project I worked on with my amateur astronomer friends in upstate New York, we developed a custom CCD control board for a Kodak sensor. This involved intricate timing and signal processing, which was made more efficient by employing modular arithmetic in our algorithms to handle cyclic data patterns.

<>

Conclusion

Modular arithmetic is a fundamental mathematical concept with far-reaching implications in cryptography and artificial intelligence. Its ability to simplify complex problems and enhance computational efficiency makes it an invaluable tool in both theoretical and applied mathematics. As we continue to explore its applications, modular arithmetic will undoubtedly remain a cornerstone of modern technological advancements, from securing data to optimizing AI algorithms.

<>

For further reading on related topics, check out my previous articles on Understanding Prime Factorization and Mitigating AI Hallucinations in Community College Classrooms.

Focus Keyphrase: modular arithmetic applications