Unlocking the Secrets of Optimization: Exploring Gradient Descent
In the realm of mathematics and computer science, the concept of optimization stands as a cornerstone for numerous advancements and innovations. Today, I dive into one of the most pivotal optimization algorithms that has significantly molded the landscape of Artificial Intelligence (AI) and Machine Learning (ML)—Gradient Descent. Having applied this very concept in developing machine learning models during my time at Harvard University, I’ve firsthand witnessed its transformative power.
Understanding Gradient Descent
Gradient Descent is an iterative optimization algorithm used to minimize a function by iteratively moving in the direction of the steepest descent as defined by the negative of the gradient. In simpler terms, it’s used to find the minimum value of a function. The beauty of Gradient Descent lies in its simplicity and efficiency, making it the algorithm of choice for many machine learning problems.
The mathematical expression for updating the parameters in Gradient Descent is:
θ = θ - α * ∇F(θ)where:
- θ represents the parameters of the function we’re trying to minimize,
- α denotes the learning rate, determining the size of the steps taken towards the minimum,
- ∇F(θ) is the gradient of the function at θ.
Application in AI and ML
In the context of AI and my specialization in Machine Learning models, Gradient Descent plays a pivotal role in training models. By minimizing the loss function, which measures the difference between the model’s predicted output and the actual output, Gradient Descent helps in adjusting the model’s parameters so that the model can make more accurate predictions.
Case Study: Machine Learning for Self-Driving Robots
During my postgraduate studies, I engaged in a project developing machine learning algorithms for self-driving robots. The challenge was to create an algorithm that could accurately predict the robot’s movements in an unknown environment. Employing Gradient Descent, we minimized the loss function of our model, which was pivotal in accurately predicting the robot’s next move based on sensor inputs.
Why Gradient Descent?
Gradient Descent is favored in machine learning due to its capability to handle large datasets efficiently. As data becomes the lifeblood of AI, the ability to process and learn from vast datasets is crucial. Gradient Descent, with its scalable nature, stands out by offering a means to effectively optimize complex models without the need for computationally expensive operations.
Visualization of Gradient Descent
Understanding Gradient Descent isn’t only about the numbers and algorithms; visualizing its process can significantly enhance comprehension. Here’s how a typical Gradient Descent optimization might look when visualized:
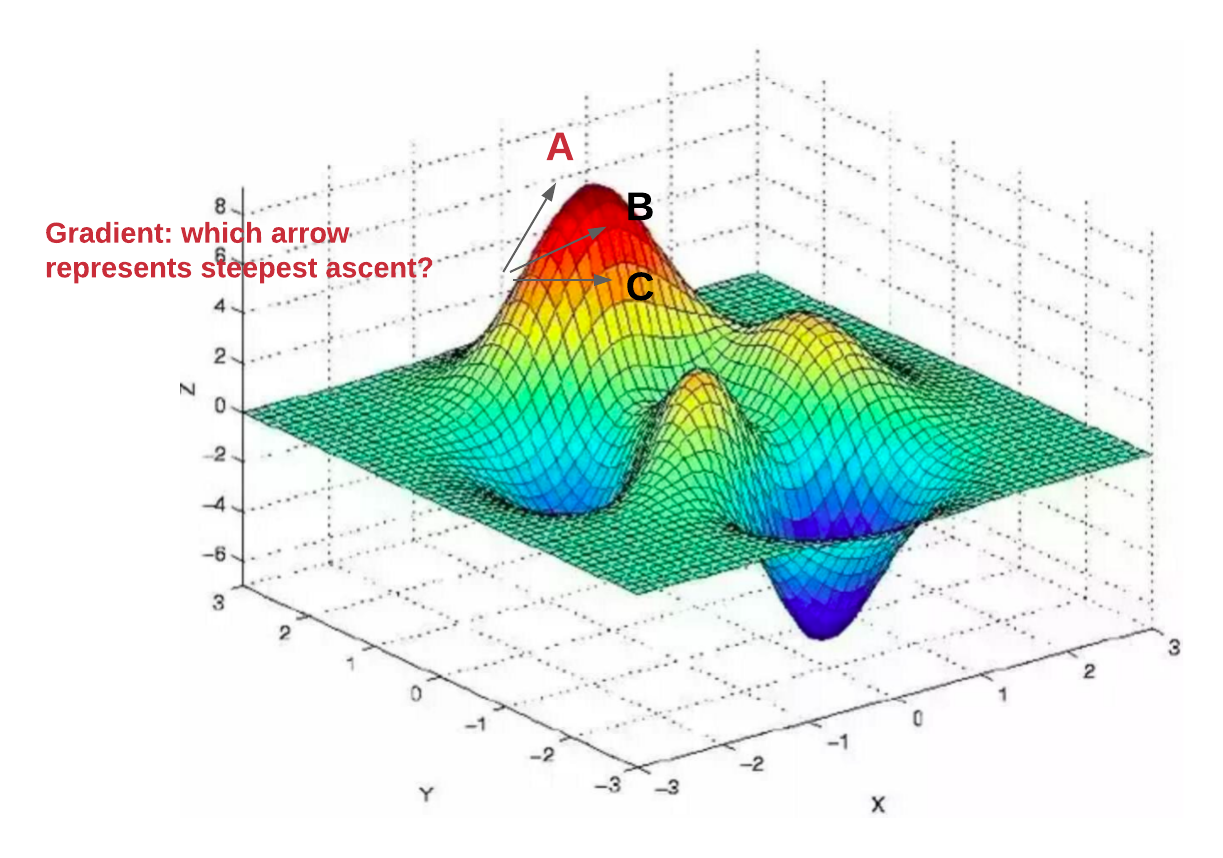
Conclusion
Gradient Descent is more than just a mathematical equation; it’s a bridge between theoretical mathematics and practical application in the field of Artificial Intelligence. As we push the boundaries of what machines can learn and do, understanding and applying concepts like Gradient Descent becomes increasingly important. In the intersection of complex algorithms and real-world applications, it continues to be a beacon of innovation, driving the development of AI and ML forward.
In the spirit of continuous exploration, I invite readers to delve deeper into how optimization techniques are revolutionizing other fields. Consider visiting my previous posts on Numerical Analysis and its significant impact on AI and machine learning for further reading.