Tag Archive for: Gradient Descent

Understanding the Role of Calculus in Neural Networks for AI Advancement

Exploring the Mathematical Foundations of Neural Networks Through Calculus

In the world of Artificial Intelligence (AI) and Machine Learning (ML), the essence of learning rests upon mathematical principles, particularly those found within calculus. As we delve into the intricacies of neural networks, a foundational component of many AI systems, we uncover the pivotal role of calculus in enabling these networks to learn and make decisions akin to human cognition. This relationship between calculus and neural network functionality is not only fascinating but also integral to advancing AI technologies.

The Role of Calculus in Neural Networks

At the heart of neural networks lies the concept of optimization, where the objective is to minimize or maximize an objective function, often referred to as the loss or cost function. This is where calculus, and more specifically the concept of gradient descent, plays a crucial role.

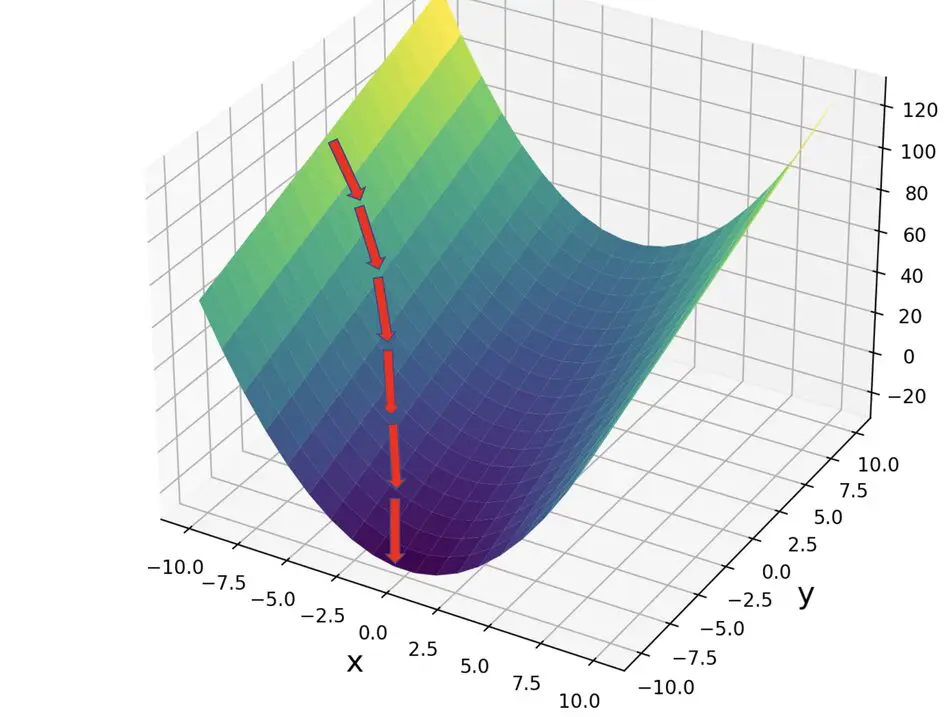
Gradient descent is a first-order optimization algorithm used to find the minimum value of a function. In the context of neural networks, it’s used to minimize the error by iteratively moving towards the minimum of the loss function. This process is fundamental in training neural networks, adjusting the weights and biases of the network to improve accuracy.

Gradient descent visualization

Understanding Gradient Descent Mathematically

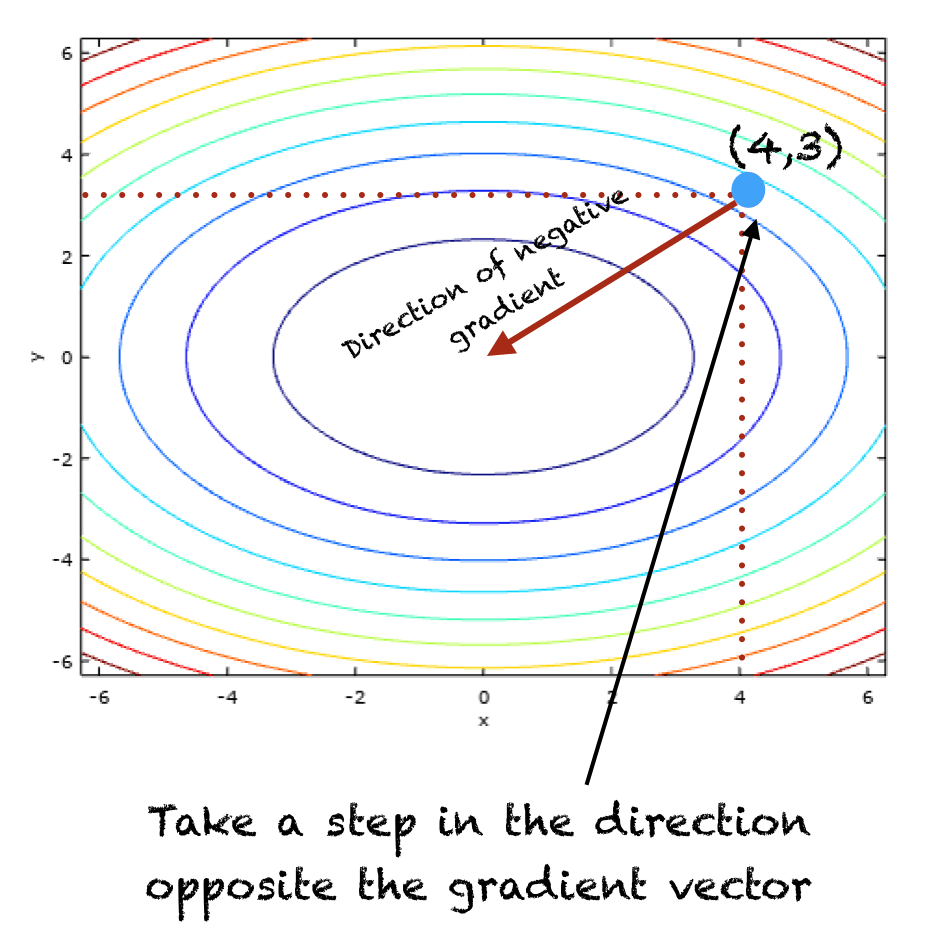
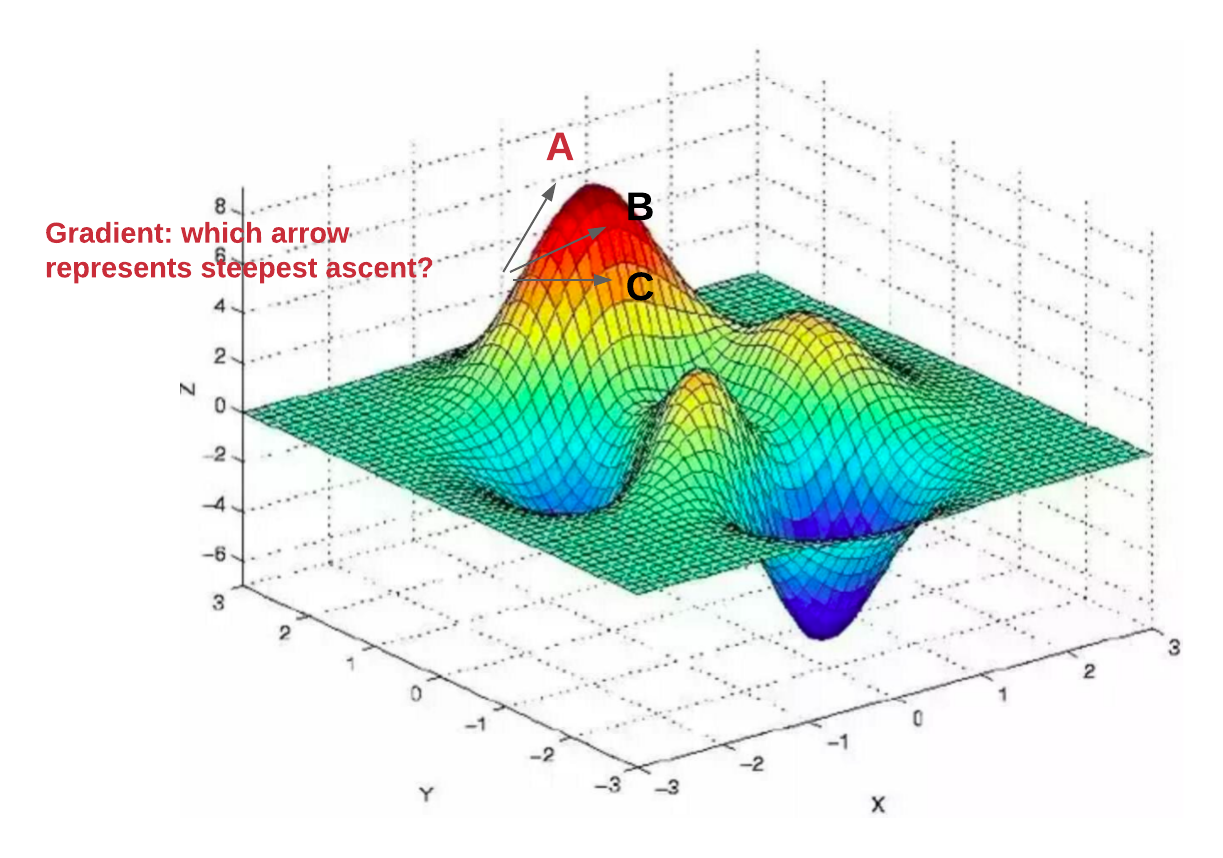
The method of gradient descent can be mathematically explained using calculus. Given a function f(x), its gradient ∇f(x) at a point x is a vector pointing in the direction of the steepest increase of f. To find the local minimum, one takes steps proportional to the negative of the gradient:

xnew = xold – λ∇f(xold)

Here, λ represents the learning rate, determining the size of the steps taken towards the minimum. Calculus comes into play through the calculation of these gradients, requiring the derivatives of the cost function with respect to the model’s parameters.

Practical Application in AI and ML

As someone with extensive experience in developing AI solutions, the practical application of calculus through gradient descent and other optimization methods is observable in the refinement of machine learning models, including those designed for process automation and the development of chatbots. By integrating calculus-based optimization algorithms, AI models can learn more effectively, leading to improvements in both performance and efficiency.

Machine learning model training process

Linking Calculus to AI Innovation

Previous articles such as “Understanding the Impact of Gradient Descent in AI and ML” have highlighted the crucial role of calculus in the evolution of AI and ML models. The deep dive into gradient descent provided insights into how fundamental calculus concepts facilitate the training process of sophisticated models, echoing the sentiments shared in this article.

Conclusion

The exploration of calculus within the realm of neural networks illuminates the profound impact mathematical concepts have on the field of AI and ML. It exemplifies how abstract mathematical theories are applied to solve real-world problems, driving the advancement of technology and innovation.

As we continue to unearth the capabilities of AI, the importance of foundational knowledge in mathematics, particularly calculus, remains undeniable. It serves as a bridge between theoretical concepts and practical applications, enabling the development of AI systems that are both powerful and efficient.

Real-world AI application examples

Focus Keyphrase: calculus in neural networks

/2 Comments/by

Understanding the Impact of Gradient Descent in AI and ML

The Integral Role of Calculus in Artificial Intelligence and Machine Learning

In the vast and constantly evolving fields of Artificial Intelligence (AI) and Machine Learning (ML), the significance of foundational mathematical concepts cannot be overstated. Among these, Calculus, specifically, plays a pivotal role in shaping the algorithms that are at the heart of AI and ML models. In this article, we’ll delve into a specific concept within Calculus that is indispensable in AI and ML: Gradient Descent. Moreover, we will illustrate how this mathematical concept is utilized to solve broader problems, a task that aligns perfectly with my expertise at DBGM Consulting, Inc.

Understanding Gradient Descent

Gradient Descent is a first-order iterative optimization algorithm used to minimize a function. In essence, it involves taking small steps in the direction of the function’s steepest descent, guided by its gradient. The formula used to update the parameters in Gradient Descent is given by:

θ = θ - α ∇θ J(θ)

where:

  • θ represents the parameters of the function or model.
  • α is the learning rate, determining the size of the steps taken.
  • ∇θ J(θ) is the gradient of the objective function J(θ) with respect to the parameters θ.

This optimization method is particularly vital in the field of ML, where it is used to minimize the loss function, adjusting the weights of the network to improve prediction accuracy.

Application in AI and ML

Considering my background in developing machine learning models for self-driving robots at Harvard University, the application of Gradient Descent is a daily reality. For instance, in ensuring that an autonomous vehicle can correctly interpret its surroundings and make informed decisions, we optimize algorithms to discern patterns within vast datasets, an endeavor where Gradient Descent proves invaluable.

Gradient Descent example in machine learning

The iterative nature of Gradient Descent, moving steadily towards the minimum of a function, mirrors the process of refining an AI model’s accuracy over time, by learning from data and adjusting its parameters accordingly. This optimization process is not just limited to robotics but extends across various domains within AI and ML such as natural language processing, computer vision, and predictive analytics.

Connecting Calculus to Previous Discussions

In light of our prior exploration into concepts like Large Language Models (LLMs) and Bayesian Networks, the underpinning role of Calculus, especially through optimization techniques like Gradient Descent, reveals its widespread impact. For example, optimizing the performance of LLMs, as discussed in “Exploring the Future of Large Language Models in AI and ML,” necessitates an intricate understanding of Calculus to navigate the complexities of high-dimensional data spaces effectively.

Moreover, our delve into the mathematical foundations of machine learning highlights how Calculus not only facilitates the execution of complex algorithms but also aids in conceptualizing the theoretical frameworks that empower AI and ML advancements.

Conclusion

Gradient Descent exemplifies the symbiotic relationship between Calculus and the computational models that drive progress in AI and ML. As we continue to push the boundaries of what AI can achieve, grounding our innovations in solid mathematical understanding remains paramount. This endeavor resonates with my vision at DBGM Consulting, where leveraging deep technical expertise to solve real-world problems forms the cornerstone of our mission.

Focus Keyphrase: Gradient Descent in AI and ML

/2 Comments/by

Exploring Gradient Descent: The Heart of AI and ML Optimization

Unlocking the Secrets of Optimization: Exploring Gradient Descent

In the realm of mathematics and computer science, the concept of optimization stands as a cornerstone for numerous advancements and innovations. Today, I dive into one of the most pivotal optimization algorithms that has significantly molded the landscape of Artificial Intelligence (AI) and Machine Learning (ML)—Gradient Descent. Having applied this very concept in developing machine learning models during my time at Harvard University, I’ve firsthand witnessed its transformative power.

Understanding Gradient Descent

Gradient Descent is an iterative optimization algorithm used to minimize a function by iteratively moving in the direction of the steepest descent as defined by the negative of the gradient. In simpler terms, it’s used to find the minimum value of a function. The beauty of Gradient Descent lies in its simplicity and efficiency, making it the algorithm of choice for many machine learning problems.

The mathematical expression for updating the parameters in Gradient Descent is:

θ = θ - α * ∇F(θ)

where:

  • θ represents the parameters of the function we’re trying to minimize,
  • α denotes the learning rate, determining the size of the steps taken towards the minimum,
  • ∇F(θ) is the gradient of the function at θ.

Application in AI and ML

In the context of AI and my specialization in Machine Learning models, Gradient Descent plays a pivotal role in training models. By minimizing the loss function, which measures the difference between the model’s predicted output and the actual output, Gradient Descent helps in adjusting the model’s parameters so that the model can make more accurate predictions.

Case Study: Machine Learning for Self-Driving Robots

During my postgraduate studies, I engaged in a project developing machine learning algorithms for self-driving robots. The challenge was to create an algorithm that could accurately predict the robot’s movements in an unknown environment. Employing Gradient Descent, we minimized the loss function of our model, which was pivotal in accurately predicting the robot’s next move based on sensor inputs.

Why Gradient Descent?

Gradient Descent is favored in machine learning due to its capability to handle large datasets efficiently. As data becomes the lifeblood of AI, the ability to process and learn from vast datasets is crucial. Gradient Descent, with its scalable nature, stands out by offering a means to effectively optimize complex models without the need for computationally expensive operations.

Visualization of Gradient Descent

Understanding Gradient Descent isn’t only about the numbers and algorithms; visualizing its process can significantly enhance comprehension. Here’s how a typical Gradient Descent optimization might look when visualized:

Gradient Descent visualization

Conclusion

Gradient Descent is more than just a mathematical equation; it’s a bridge between theoretical mathematics and practical application in the field of Artificial Intelligence. As we push the boundaries of what machines can learn and do, understanding and applying concepts like Gradient Descent becomes increasingly important. In the intersection of complex algorithms and real-world applications, it continues to be a beacon of innovation, driving the development of AI and ML forward.

In the spirit of continuous exploration, I invite readers to delve deeper into how optimization techniques are revolutionizing other fields. Consider visiting my previous posts on Numerical Analysis and its significant impact on AI and machine learning for further reading.

/0 Comments/by
Link to: Get in touch

Let’s collaborate!

Contact Me

DAVID MAIOLO

 The content on this website, including text, photographs, and any other media, is the property of David Maiolo unless otherwise noted. No part of this website may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the owner.

DISCLAIMER

The information provided on this website is for general informational purposes only. While I strive to keep the information up-to-date and correct, I make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will I be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. *This website may include links to other websites which are not under the control of David Maiolo. I have no control over the nature, content, and availability of those sites.

© 2024 David Maiolo