“`html

The Elegance of Numerical Methods in AI Predictive Models

In the realm of Artificial Intelligence and Machine Learning, precision and accuracy are paramount. It’s here that numerical analysis not only finds its application but also shines, bridging the gap between theoretical models and real-world data. As a consultant specializing in AI, I’ve witnessed firsthand the transformative power of numerical methods in predictive modeling.

Understanding Numerical Analysis

Numerical analysis is a branch of mathematics that devises, analyzes, and implements algorithms for obtaining numerical solutions to problems inherent in continuous mathematics. This discipline is the backbone of computational models, especially in areas requiring the solution of complex equations that are difficult or impossible to solve analytically.

Case Study: Solving Differential Equations

One of the most compelling examples of numerical analysis in action is in solving differential equations for predictive models. Differential equations are vital in modeling real-world processes in physics, engineering, and notably, in AI predictive models. The Role of Differential Equations in Enhancing AI Predictive Models further elucidates their importance.

Numerical Methods for Differential Equations

There are several numerical methods available for solving differential equations, such as Euler’s method, the Runge-Kutta methods, and the finite element method. Each has its advantages and specific use cases, but all serve the purpose of approximating solutions to otherwise intractable models.

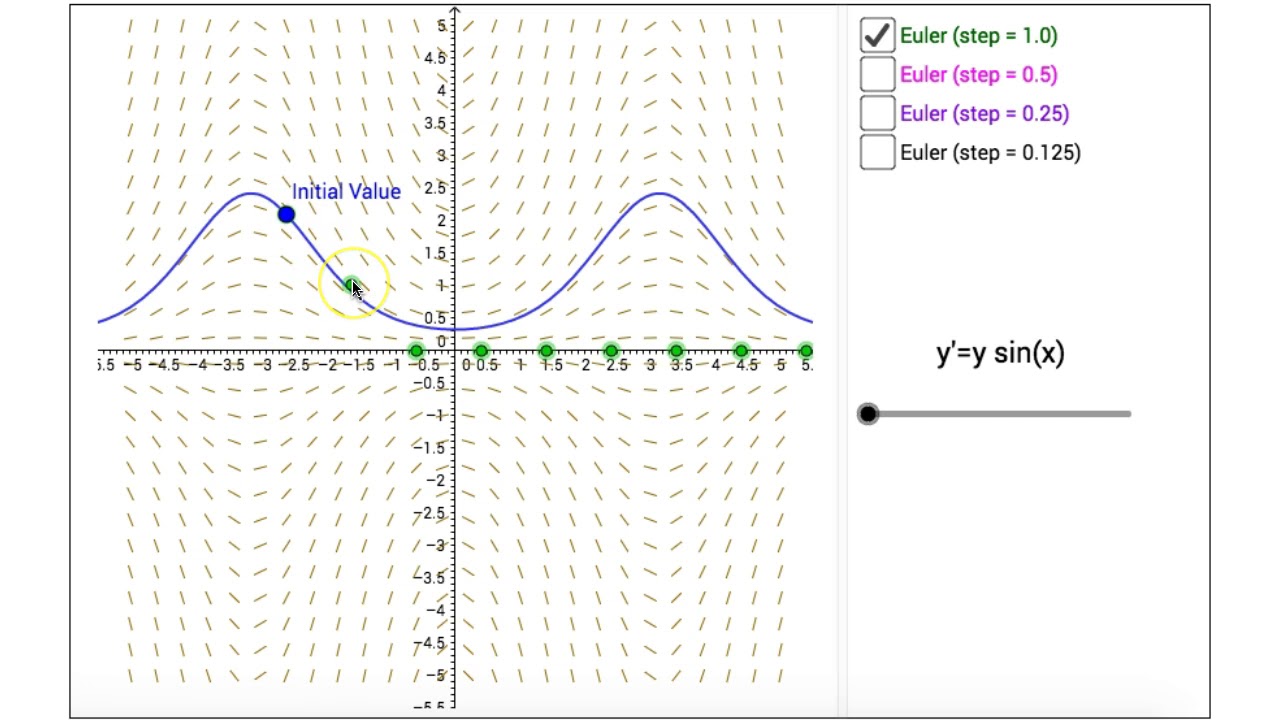
Let’s delve a bit deeper into Euler’s method, a fundamental numerical approach for solving ordinary differential equations (ODEs). It proceeds as follows:

• Given an initial value problem \(y’=f(t,y), y(t_0)=y_0\),
• Euler’s method approximates y at subsequent points by \(y_{n+1} = y_n + h*f(t_n, y_n)\),
• where \(h\) is the step size and \(t_{n+1} = t_n + h\).

Although simple, Euler’s method lays the foundation for more complex algorithms and illustrates the fundamental idea of progressing step-wise to approximate solutions over a range.

Applying Numerical Methods in AI

My experience at DBGM Consulting, Inc., particularly in developing machine learning models for self-driving robots, highlighted the indispensability of numerical methods. For instance, optimizing pathfinding algorithms or sensor data interpretations invariably resorts to solving differential equations, for which numerical analysis provides the tools.

Numerical analysis, especially in AI, isn’t just about finding solutions—it’s also about ensuring these solutions are computationally feasible and aligned with real-world data. In essence, numerical methods help translate mathematical models into actionable intelligence, crucial for anything from process automation to predictive modeling.

Conclusion

The fusion of numerical analysis with AI and machine learning brings forth solutions that are both innovative and grounded in mathematical rigor. As someone who has navigated the intersection of technology, mathematics, and real-world application, I assert the value of numerical methods is immeasurable. They empower us to solve complex problems, optimize algorithms, and ultimately, drive forward the frontier of what’s possible in AI and beyond.

“`