Tag Archive for: Computational Algorithms

The Intriguing Role of Regex in Prime Number Detection and AI

The Curious Case of Regular Expressions and Prime Numbers

Prime numbers have fascinated mathematicians for centuries, holding a central place in the foundation of number theory and cryptography. From my background in artificial intelligence and computational systems, I tend to look for practical methods and efficient algorithms to address challenges. However, encountering a seemingly “magical” method to identify prime numbers through purely symbolic means, like regular expressions (or regex), piqued my skeptic yet intrigued mind.

Demystifying the Regex-based Prime Test

The use of regex to determine whether a number is prime may appear esoteric at first. After all, regular expressions are typically used to match strings and patterns in text, not perform arithmetic. The trick lies in how you interpret the input and the clever use of regex syntax and constructs.

This particular prime-checking regex query operates in Python, a language widely used in AI and data science, and involves transforming a number into a specific string form—a tally of ones, for example. Simply put, this process interprets numbers as strings of repeated characters like “1”. It then attempts to break this string down using regular expression patterns to see if it can exactly divide into subgroups, which corresponds to finding whether a number has any divisors other than one and itself. If it does, it is composite; if not, it is prime.

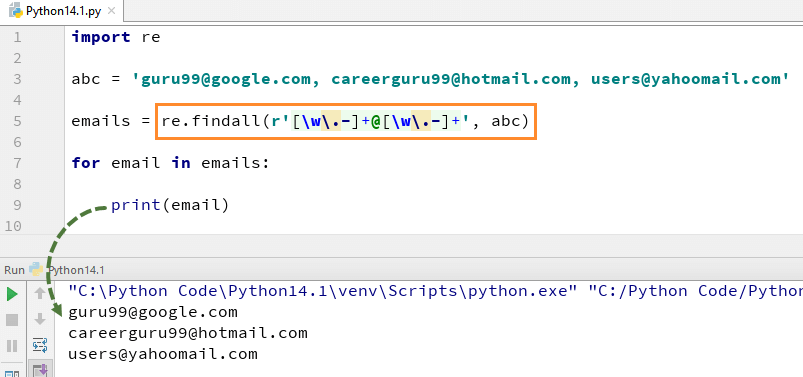Breaking Down the Regex Symbols

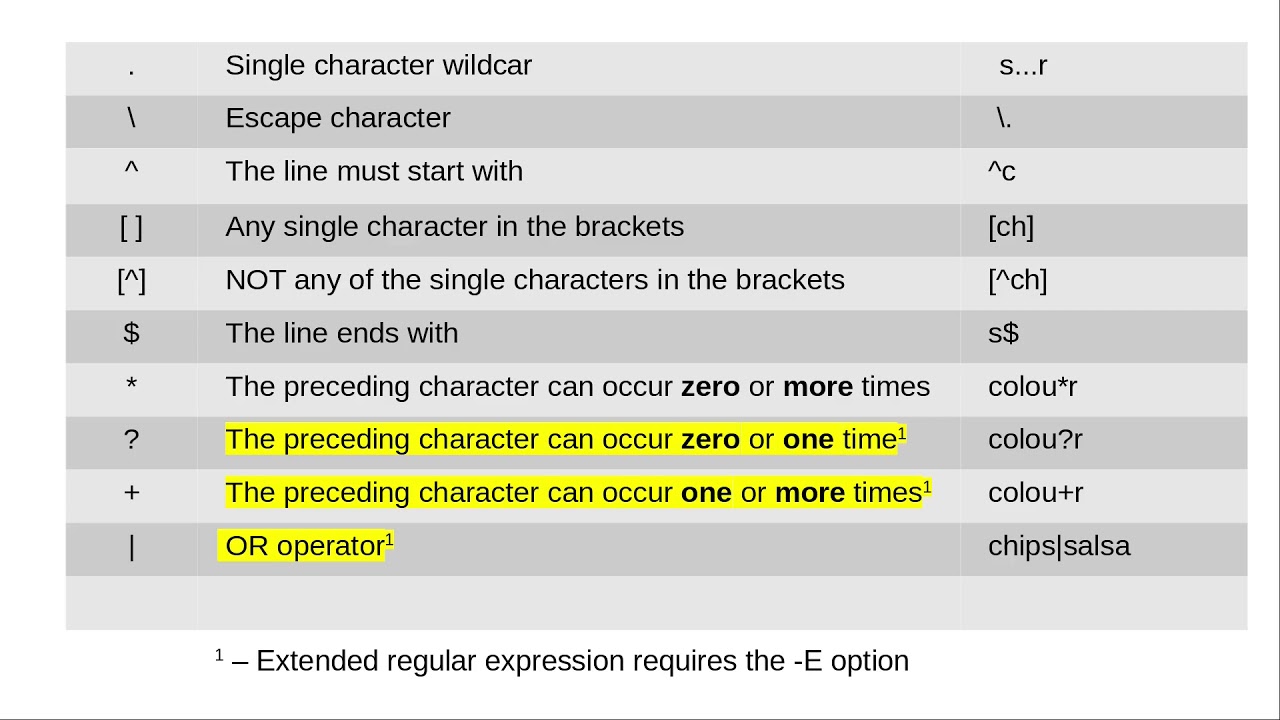
For those unfamiliar with regex syntax, the following can make the prime detection process less “spooky” (though perfect for a Halloween-themed discussion):

A dot . represents any character (a wildcard).
A plus + means “one or more” of the previous element.
The question mark ? makes the matching process “lazy”, stopping at the shortest possible string that matches the regex pattern.
Up arrows ^ and dollar signs $ indicate the start and end of a string, ensuring the entire sequence is examined.
The forward slash notation \1 calls back to a previous match, allowing the system to reuse prior captured groups—key in testing factors for the number in question.

By leveraging these symbols, regex can efficiently decompose each string of ones (whether it’s “11”, “111”, “1111”, etc.), and check how many ways the string can be evenly rerun back against itself. When no such division exists, the original number is prime.

A Surprisingly Efficient Algorithm?

One might assume that this method wouldn’t scale well for larger numbers due to the inefficiency of regex at such a task. However, optimizing the string breakdown process—such as using lazy matching—enables this algorithm to avoid some performance hits. It’s an interesting contrast to traditional Sieve of Eratosthenes approaches for prime detection. While regex isn’t typically designed for numerical computation, this clever use shows the linguistic flexibility programming languages like Python offer.

As a former Microsoft Solutions Architect specializing in cloud migration, I’ve often dealt with automation and optimization techniques. Here, Python’s built-in re library handles the brute force nature of regex effectively, which I compare to the optimizations I’ve worked on within AI models for process efficiency and computational scaling.

Regular Expressions in the Broader Tech Ecosystem

Aside from mathematical curiosities like prime testing, regex plays an important role in modern computing, especially in information retrieval systems. In previous work on AI search models, for instance, regex patterns are used to streamline database queries or identify information patterns within massive datasets. When scaling or migrating these solutions to the cloud, regex becomes part of the toolkit to ensure data is cleanly parsed, matched, or processed for machine learning models.

It All Goes Back to Probability

For readers familiar with my earlier articles on math and probability theory, tying these subjects back to regex patterns might seem unexpected. But probability theory and prime numbers share fundamental connections, especially in cryptography and number theory, where prime distribution characterizes randomness.

While regex might open a symbolic window into prime numbers, it raises a fundamental question: Can symbolic reasoning and pattern-matching methods replace traditional number theory methods in advanced AI or cryptographic functions? The answer, as always, remains nuanced. However, blending computational models like regex with AI frameworks already shows promise in enhancing algorithmic capabilities, such as in machine learning case studies I’ve worked on, where pattern recognition significantly accelerates problem-solving.

Conclusion

Regular expressions may not be the final frontier in prime number research, nor are they likely to replace more optimized algorithmic efficiency tools like the Sieve of Eratosthenes for large-scale computations. But as this clever symbolic solution demonstrates, the lines between symbolic manipulation and numerical computation continue to blur. And in the realm of artificial intelligence, where pattern recognition reigns supreme, methods like regex may prove unexpectedly useful when solving unique computational challenges.

Straddling both the realms of programming and number theory, regex offers us yet another glimpse into the interconnectivity of languages—whether spoken, mathematical, or computational. It’s a great reminder of how diverse techniques can emerge from seemingly unrelated fields, much in the same way as cosmic events can affect technological advances.

Focus Keyphrase: regex prime number detection

November 15, 2024/2 Comments/by David Maiolo

Artificial Intelligence (AI)

Exploring Wolfram’s Theory of Everything: Can the Universe Be a Giant Computer Program?

Exploring Wolfram’s Theory of Everything: Could the Universe Be a Giant Computer Program?

For several years, I’ve been asked to explore Stephen Wolfram’s “Theory of Everything”—a bold attempt to describe the fundamental workings of the universe through computational theory. Wolfram, a renowned computer scientist and creator of the popular Mathematica software, proposes that the universe operates like a computer program. What if, at its core, the universe follows a set of simple computational rules that give rise to the complex phenomena we observe today such as gravity, the Standard Model, and relativity? This notion connects closely to the simulation hypothesis, which speculates that our reality is a giant simulation. It’s an intriguing theory, but does it hold up under scientific scrutiny?

The Simulation Hypothesis and Computation in Physics

The basic idea behind Wolfram’s theory is simple, yet profound: the universe follows a set of fundamental rules, not unlike a computer algorithm. From these basic rules, everything—from the force of gravity to the behavior of subatomic particles—emerges. Wolfram’s approach is based on similar principles that underpin cellular automaton, where simple rules can generate surprisingly complex patterns.

But can we actually explain physics with computation? Wolfram suggests that you could conceptualize the universe in a manner similar to a cellular automaton—essentially a four-dimensional “code” that evolves step by step. This would mean that all aspects of the universe are, at some level, deterministic and computationally structured. Yet, despite the elegance of this idea, it faces significant hurdles when subjected to the rigorous demands of physics, particularly Einstein’s theory of relativity.

Challenges with General Relativity and Lorentz Symmetry

The main challenge with Wolfram’s theory is its compatibility with Einstein’s General Relativity. Relativity describes how space and time are intimately connected and varies based on an observer’s reference frame. One major problem with computational approaches is that they work in discrete steps—increments of space and time. However, according to relativity, these increments can’t remain hidden. If space and time were truly discrete, this would manifest observationally. Yet, there’s no evidence of such discreteness.

In an elegant illustration, think of a photon—a quantum of light. The energy of the photon depends on how it’s observed: its energy is higher if the observer is moving towards it, lower if moving away. In an inherently discrete computational model, issues arise because different observers would calculate unobserved gaps in the graph representing space. This disconnect prevents any computational model from approximating General Relativity in a way that respects all of Einstein’s symmetries.

This brings us to the concept of Lorentz Symmetry, a key pillar of General Relativity that ensures the same physical laws apply regardless of how fast you’re moving or where you are in space. Attempting to simulate this through computational methods like grids, graphs, or even Wolfram’s hypergraphs has, thus far, proven problematic.

Introducing Hypergraphs: A Way Forward?

Despite the difficulties, Wolfram has pressed forward and introduced the idea of hypergraphs as a potential solution. A hypergraph is a more complex version of a traditional graph, where sets of nodes (representing points in space-time) are connected in ways that circumvent the discretization problems of simpler models. According to Wolfram, hypergraphs may offer a way to reconcile computation with both space and matter without breaking the theory of relativity.

In 2020, Wolfram and his collaborators published a follow-up to address concerns about Lorentz symmetry. They’ve focused on how hypergraphs might solve the problem of preserving the symmetry requirements of relativity in a discrete structure. In principle, this should work similarly to another theory in physics known as “causal sets,” a respected attempt to describe space and time as a network of discrete points with causal relationships between them.

At this juncture, it’s worth noting that while Wolfram’s hypergraphs offer a clever solution, they still leave much unexplained. For instance, his framework for quantum mechanics, the behavior of elementary particles, and how exactly the Standard Model fits into the picture remains vague. This is an area I hope to see more developments on, as successful integration here would truly validate or break his theory’s foundation.

Looking Ahead: Are We Near a Theory of Everything?

Wolfram’s theory is an ongoing, evolving effort, and it’s not without merit. At the very least, it introduces novel approaches to theoretical physics and stimulates some intriguing discussions. However, it hasn’t reached a point where it effectively competes with established theories like General Relativity or String Theory. Incorporating quantum physics and providing stringent mathematical proofs for his model remains a significant challenge. Time will tell whether Wolfram’s work is able to capture the attention of mainstream physicists or if it will remain a curious side-note in the long and complicated quest for a “Theory of Everything.”

In conclusion, Wolfram’s theory is an ambitious attempt to bring the simulation hypothesis into the realm of physics. Does it answer all the questions? Certainly not yet. But given the originality and clarity of thought, it’s certainly worth paying more attention to. Perhaps, like many groundbreaking ideas, it will slowly gain traction as physicists grapple with its implications over time.

Relating to Previous Discussions on Fundamental Physics

Readers following my previous articles on quantum physics such as “Loop Quantum Gravity vs. String Theory” or on advances in “Understanding String Theory”, might notice a through line: physicists globally continue to grapple with how to marry quantum mechanics with relativity. Wolfram’s theory raises many of the same questions addressed in string theory, yet ventures into completely new territory by attempting to use computational rules to explain everything. Similar to how loop quantum gravity discretizes space-time, Wolfram’s hypergraph approach seeks to unify fundamental physics but with a key computational twist.

The importance of finding a Theory of Everything cannot be overstated. It’s the holy grail of physics. Whether Wolfram’s computational universe is that missing link remains an open question, but it certainly warrants more attention as physicists and mathematicians further explore it.

Focus Keyphrase: Wolfram’s Theory of Everything

October 25, 2024/2 Comments/by David Maiolo

AI Projects

Revolutionary Advances in Elastic Body Simulations: Breakthroughs in Real-Time Soft Matter Modeling

Revolutionary Advances in Elastic Body Simulations: The Future of Soft Matter Modeling

Simulating the behavior of elastic bodies has long posed a monumental challenge in both computer graphics and physics. The sheer complexity of accurately modeling millions of soft body interactions in real time is nothing short of a scientific marvel. Advances in computational algorithms, especially those focused on elastic body simulations, have made it possible to visualize and simulate dynamic environments that seem impossible at scale. Recent breakthroughs have transformed this area, enabling simulations that can handle thousands, even millions, of collisions with breathtaking realism and speed.

How Elastic Body Simulations Work

At the core of elastic body modeling lies the ability to simulate objects that deform under external forces but return to their original shape when those forces are removed. Imagine stuffing a bunch of soft, squishy objects—like small rubber balls—into a confined space such as a teapot. In real life, the balls would compress, interact with each other, and shift within the confines of the pot. This is the basic idea behind elastic body simulation: performing millions of individual calculations to account for each collision, deformation, and rebound, all at once.

Layer on more complexity—for instance, an airport filled with one million individuals moving about—and suddenly the task becomes exponentially more difficult. Not only do you need to account for individual movements, but also for the subtle forces at play when objects (or people) bump into and influence each other in real time.

Major Breakthroughs in Speed and Stability

Recent research has unveiled a remarkable technique that subdivides a large problem into smaller, more manageable ones, drastically improving simulation speed. At its base, this method uses Gauss-Seidel iterations, which effectively solve these smaller, interrelated problems in parallel. Imagine trying to fix a chair while sitting on it—it sounds impossible, but that’s essentially what this method does with exceptional success.

In prior techniques, simulating such a scenario—even small aspects of it—could take hours or days. Today, thanks to advancements in elastic body engine technology, these impossibly complex simulations can now be completed in mere seconds per frame.

“Many of these simulations in modern graphics engines deal with 50 million vertices and 150 million tetrahedra. Each vertex is like a node in a network, and each tetrahedron a mini atomic structure. Think about packing this complexity into tangible, interacting materials—while maintaining computational stability.”

Testing the Limits of Soft Body Simulation

Elastic body simulations have been pushed to their absolute limits with tests that include objects interacting under extreme conditions—take, for instance, a series of octopi and armadillos pushed into a glass enclosure. These creatures are soft by nature, and seeing them respond to compression and collision in such a detailed manner highlights how advanced this simulation technology has become. Imagine stacking millions of small, compressible objects on top of each other and needing every point of contact to behave as it should. No shortcuts allowed.

The Miracle of Bouncing Back

Compressed an elastic body too far? No problem. The new breakthrough algorithms ensure the object returns to form after extreme force is removed, showcasing an impressive level of detail. The stability of simulations has reached a point where researchers can pull, stretch, squish, and compress objects without breaking the underlying computational model. In an era when graphics engines are expected to push boundaries, it’s remarkable to see this kind of fidelity, especially when you remember that no part of the simulation can “cheap out” on underlying physics.

Application in the Real World

Old Techniques	Modern Techniques
Slow calculation times (hours or days)	Real-time simulations (seconds per frame)
Poor stability under extreme conditions	Highly stable, regardless of compression or stretching
Limited object interaction precision	Accurate modeling of millions of vertices and tetrahedra

These breakthroughs do more than just create incredible digital imagery for movies or video games—they have real-world applications in engineering, medical technology, and even disaster modeling. Industries that rely on understanding soft matter interactions—such as biomechanics, robotics, and materials science—are particularly excited about these simulations. Whether simulating how a shoe sole compresses underfoot, or modeling crash tests with soft bodies, having this level of computational accuracy and speed revolutionizes how products are developed, tested, and ultimately brought to market. This is core to the concept of “engineering simulations” I often discuss in seminars we host through DBGM Consulting.

The Future: Faster and Better

One of the most mind-blowing aspects of these modern simulations is not just their speed but also their immense stability. Testing has shown that these engines can be up to 100-1000x faster than previous computation models, which fundamentally changes what is possible in real-time simulations. Imagine simulating the deformation and interaction of buildings, cars, or crowded stadiums filled with people—all with precise accuracy.

Most fascinating, the improved methods generate results on a logarithmic scale rather than a linear one, meaning the computational speed and efficacy increase exponentially. This has major implications for fields both inside and outside computer graphics, from AI-driven robotic design to large-scale astrophysical simulations.

In past articles, we have discussed mathematical frameworks such as string theory and even the foundational role numbers play in fields such as machine learning and artificial intelligence (The Essential Role of Foundational Math in AI). It’s incredible to see how these seemingly abstract principles of number theory and physics now play crucial roles in real-world technologies, such as soft body simulations.

A Look Ahead

With astonishing advancements in both speed and stability, it’s an exciting time to be involved in computational sciences and design. These new elastic body simulation techniques don’t just push the boundaries of what is possible—they redefine them altogether. It is a major leap forward, not just for entertainment but for every industry where complex object interaction is relevant, whether it’s automotive design (a personal passion of mine) or astronomy simulations, as we explore with my group of friends in Upstate NY using high-end CCD cameras to capture deep space phenomena.

With the right algorithms, hardware, and expertise, we now have the ability to create and manipulate synthetic worlds with unparalleled precision, opening doors to innovation that were previously only dreamed of.

Loving it!

For more exciting discussions on advancements in simulation and other emerging technologies, check out my previous post diving deeper into the breakthrough of Elastic Body Simulation for High-Speed Precision.

Focus Keyphrase: Elastic Body Simulations

October 22, 2024/2 Comments/by David Maiolo