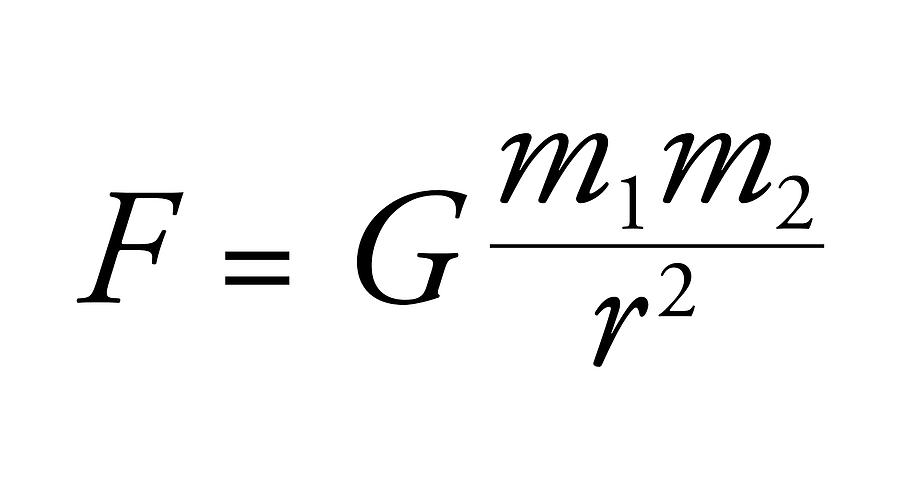As I delve into the intricacies of physics, I’m continually fascinated by the concept of acceleration – a fundamental principle that transcends the simple notion of ‘speeding up’. In my exploration of the physical world, from the macroscopic down to the quantum level, I’ve realized that acceleration is not just about how fast an object’s velocity changes; it’s a cornerstone in understanding the complexities of both linear and rotational motion. Whether it’s the graceful arc of a planet orbiting a star or the elegant spin of a dancer, acceleration is at the heart of these motions, shaping the dynamics of our universe in profound ways.
In this exploration, I aim to unravel how acceleration plays a pivotal role in various forces that govern motion. We’ll embark on a journey through different realms of physics, from the familiar gravitational pull that keeps our feet firmly on the ground, to the centripetal and centrifugal forces that rule circular motion, and even into the realm of angular momentum, which rules everything from spinning tops to swirling galaxies. Our journey will not stop there; we’ll venture into the realms of Einstein’s relativity and the mysterious quantum field theory, offering diverse perspectives on these forces. Through this, we aim to gain a deeper understanding of how acceleration, in its many forms, is woven into the very fabric of our physical reality.
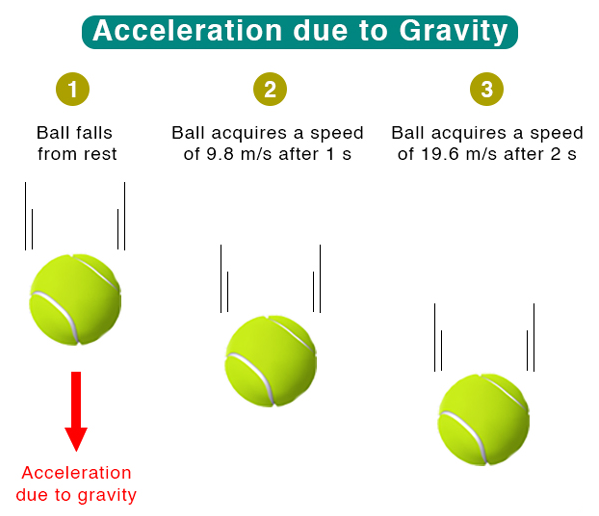
Section 1: The Fundamentals of Acceleration
In exploring the realms of motion, it’s crucial to distinguish between linear and angular acceleration, both fundamental yet distinct in their nature. Linear acceleration is straightforward; it’s a change in the velocity of an object in a straight line, easily felt as a car speeds up or slows down. Measured in meters per second squared, it quantifies how quickly an object’s speed changes along a path. Angular acceleration, on the other hand, is subtler yet omnipresent in anything that rotates. It describes the rate of change of angular velocity – a concept critical in understanding rotational motion. What’s fascinating, and often a point of misconception, is that an object in circular motion, like a spinning wheel, is constantly accelerating even if its rotational speed remains constant. This is because acceleration, in a physical sense, is not just about changes in speed; it’s about changes in velocity, which includes direction. A spinning object continually changes its direction, and hence, is always undergoing acceleration, even if the rate of its spin doesn’t increase. This distinction underscores the complex nature of motion, where even seemingly steady rotation masks a continuous state of acceleration.
Visual 2 (Table):
| Aspect |
Linear Acceleration |
Angular Acceleration |
| Definition |
Change in velocity per unit time along a line |
Change in angular velocity per unit time |
| Units |
Meters per second squared (m/s²) |
Radians per second squared (rad/s²) |
| Caused By |
Forces like gravity, friction |
Torque |
| Common Examples |
Car accelerating on a highway |
Spinning top or planet rotating around its axis |
| Measurement |
Speedometer in vehicles |
Tachometer in machinery |
| Effect on Objects |
Changes speed along a path |
Continuously changes direction of motion |
Section 2: Classical Mechanics – Newton’s Laws Revisited
Sir Isaac Newton’s laws of motion, formulated in the 17th century, are cornerstones of classical mechanics and have laid the foundation for much of our understanding of physical motion. His first law, the law of inertia, states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external force. As we see here, the box continues on as only the car is acted on a force to stop.
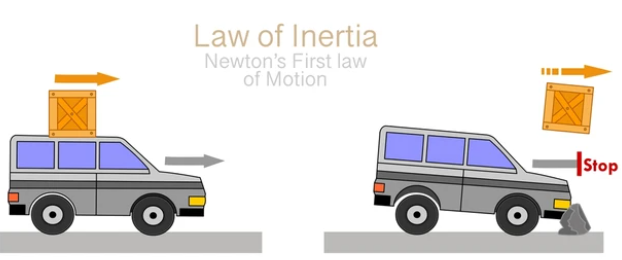
This principle is at the heart of understanding linear acceleration. Yet, it applies equally to rotational motion – a spinning object will maintain its angular velocity unless acted upon by an external torque. Think of the earth or a top spinning. They are much like the box on the car that wants to keep moving forward unless there is a force enacted on it.
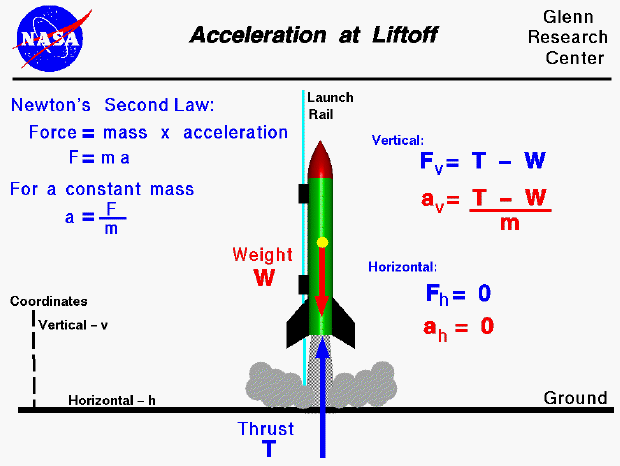
In the first law, an object will not change its motion unless a force acts on it. In Newton’s second law, the force on an object is equal to its mass times its acceleration. This second law, often written as F = ma, links force to linear acceleration. Observe how it is easier for the man to push the smaller ball. What we are saying here is that the there is a force required to get something to accelerate, and that is also dependent on how massive the object is. When you think about it, it’s quite intuitive.
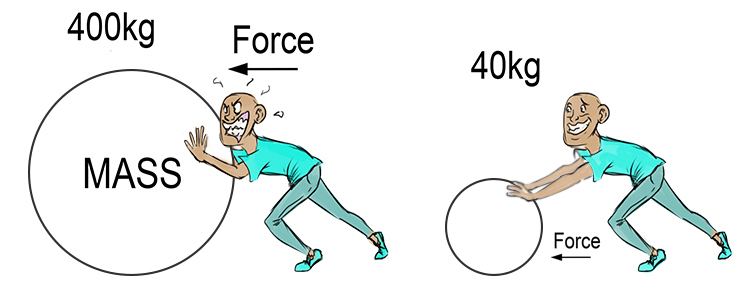
However, in the context of rotational motion, it translates to torque being equal to the product of moment of inertia and angular acceleration. So in the same scenario as pushing the ball, the force to get a wheel to accelerate will be dependent on how massive that wheel is. This is also intuitive. I imagine a giant, town sized, stone wheel would be much harder to accelerate than a bike tire.
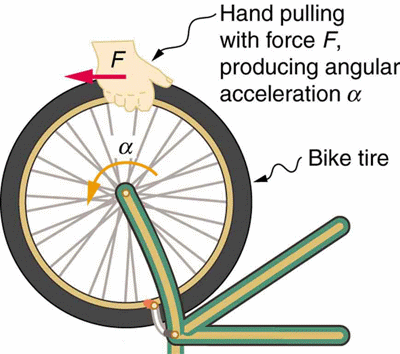
This law helps us quantify the changes in rotational motion under the influence of external forces. Curiously, Newton’s understanding of gravity as a force acting at a distance was inherently based on acceleration, although this connection was fully realized only with Einstein’s theory of General Relativity, which redefined gravity not as a force, but as the curvature of spacetime influencing the acceleration of objects.
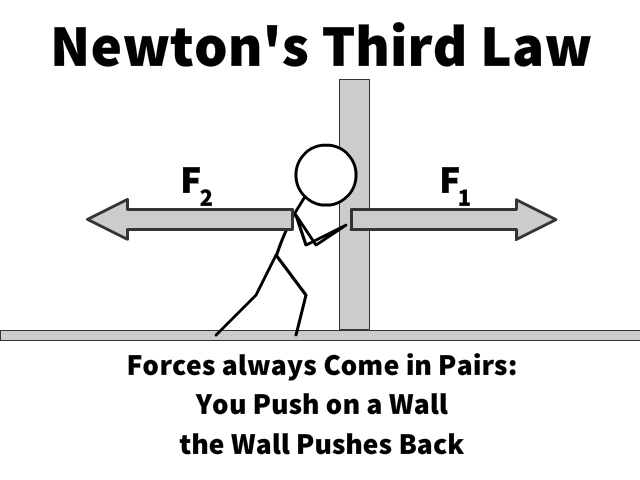
Newton’s third law, the principle of action and reaction, has its rotational counterpart as well. Just as forces result in equal and opposite reactions, a torque applied to a body will produce an equal and opposite torque. Think, when you push on a wall, it tends to wants to push back on us as well, otherwise we’d all just be able to smash down any wall.
This principle of action and reaction in rotational motion leads us directly into the fascinating realm of angular momentum, a concept in rotational dynamics analogous to linear momentum. Angular momentum in a closed system is conserved – meaning the total angular momentum before any interaction is equal to the total angular momentum afterward, provided no external torque influences the system. This conservation is crucial in explaining various phenomena, one of the most visually intuitive being the behavior of an ice skater spinning on ice.
Imagine an ice skater beginning a spin with arms extended. In this position, the skater’s body has a certain angular momentum, determined by the rotational speed (angular velocity) and how the mass is distributed (moment of inertia). When the skater pulls in their arms, they are reducing their moment of inertia. Because there are no external torques acting (assuming ideal conditions with no friction or air resistance), the total angular momentum must remain constant. The only way to balance the equation, so to speak, is for the rotational speed to increase as the moment of inertia decreases.
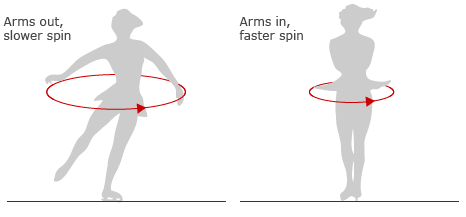
This increase in rotational speed isn’t just a mathematical outcome; it’s a vivid demonstration of the conservation of angular momentum. By pulling in their arms, the skater brings more mass closer to their axis of rotation, decreasing the moment of inertia. To compensate, the rotational speed increases, allowing the skater to spin faster. This same principle is observed in the wider cosmos, where celestial bodies exhibit changes in rotational speed due to variations in their moment of inertia, yet always adhering to the unwavering rule of angular momentum conservation.
Understanding these laws and principles in both linear and angular forms provide a comprehensive picture of the mechanics governing motion in our universe.
Section 3: Exploring Forces – Gravity, Centripetal, and Centrifugal
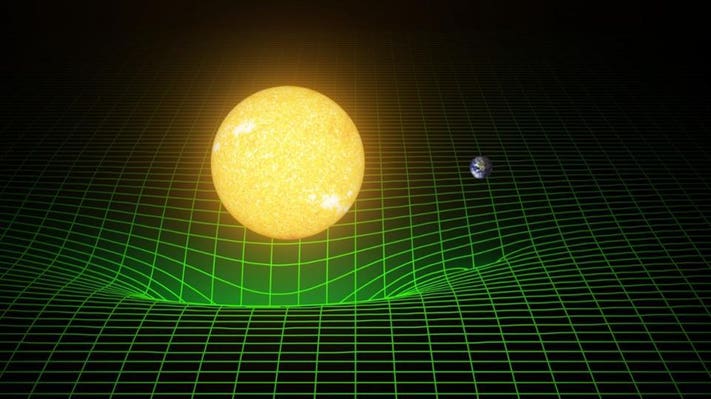
Reflecting upon Newton’s laws and the developments that followed, it becomes increasingly clear that gravity, centripetal, and centrifugal forces, while seemingly distinct, are intricately linked and are, in many ways, manifestations of the same underlying principle viewed from different perspectives. The unifying thread among these is acceleration. Historically, gravity was perceived as a mysterious force pulling apples to the ground or keeping planets in orbit. However, it wasn’t until Einstein’s theory of General Relativity that we truly understood gravity not as a force in the traditional sense, but as an effect of the curvature of spacetime – objects in free fall are actually in a state of constant acceleration, not being ‘pulled’ by a force. This revelation shifts our perspective, aligning gravity more closely with the concept of acceleration than with a conventional force.
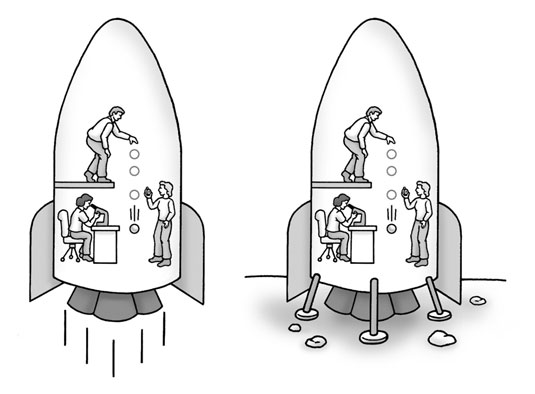
As you can see here, a spaceship on earth experiencing the acceleration of 9.8 m/s² from the curvature of spacetime is the exact same experience inside the ship as that spaceship in outer space accelerating at 9.8 m/s².
Similarly, centripetal and centrifugal forces, traditionally viewed in the context of circular motion, are deeply rooted in acceleration. Centripetal force, essential for any object moving in a circular path, is fundamentally about acceleration towards the center of the circle – consistent with Newton’s insight that a force causes acceleration. In contrast, centrifugal force, often misunderstood as a ‘real’ force, is actually an apparent force experienced in a rotating reference frame. It is the sensation of being pushed outward when in reality, it’s the inertia of the moving object – its resistance to the change in direction, which is, again, a form of acceleration.
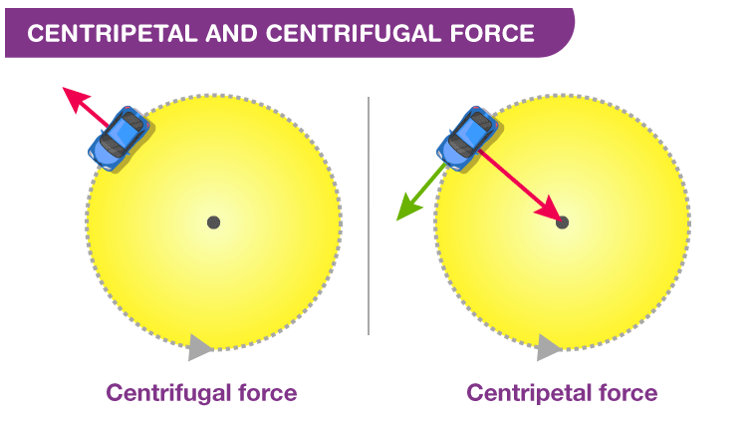
Here, acceleration is not a force per se, but it manifests as what we perceive as force, depending on our frame of reference.
Visual 4 (Table):
| Concept |
Traditional Understanding |
Modern Perspective |
Unifying Principle |
| Gravity |
A force pulling objects together. |
Curvature of spacetime causing acceleration. |
Acceleration as the effect of spacetime curvature. |
| Centripetal |
Force causing circular motion. |
Acceleration towards the center of a circular path. |
Acceleration as the cause of circular motion. |
| Centrifugal |
Force pushing objects outward in rotation. |
Apparent force due to inertia in a rotating frame. |
Acceleration (inertia) perceived as a force in a rotating frame. |
Section 4: Simulating Gravity Through Forces and Debunking Myths
The concept of using forces to simulate gravity is both fascinating and complex, with acceleration playing a pivotal role. For instance, consider the idea of continuously accelerating a spacecraft at 9.8 m/s² to mimic Earth’s gravitational pull. While theoretically sound, this method encounters a fundamental limit: as the spaceship’s velocity increases, it would eventually approach the speed of light, a scenario that defies the laws of physics as defined by Einstein’s theory of relativity. To help understand why, when we say “9.8 m/s²”, we are saying the spaceship is feeling acceleration at 9.8m/s faster than it did the second before, forever!
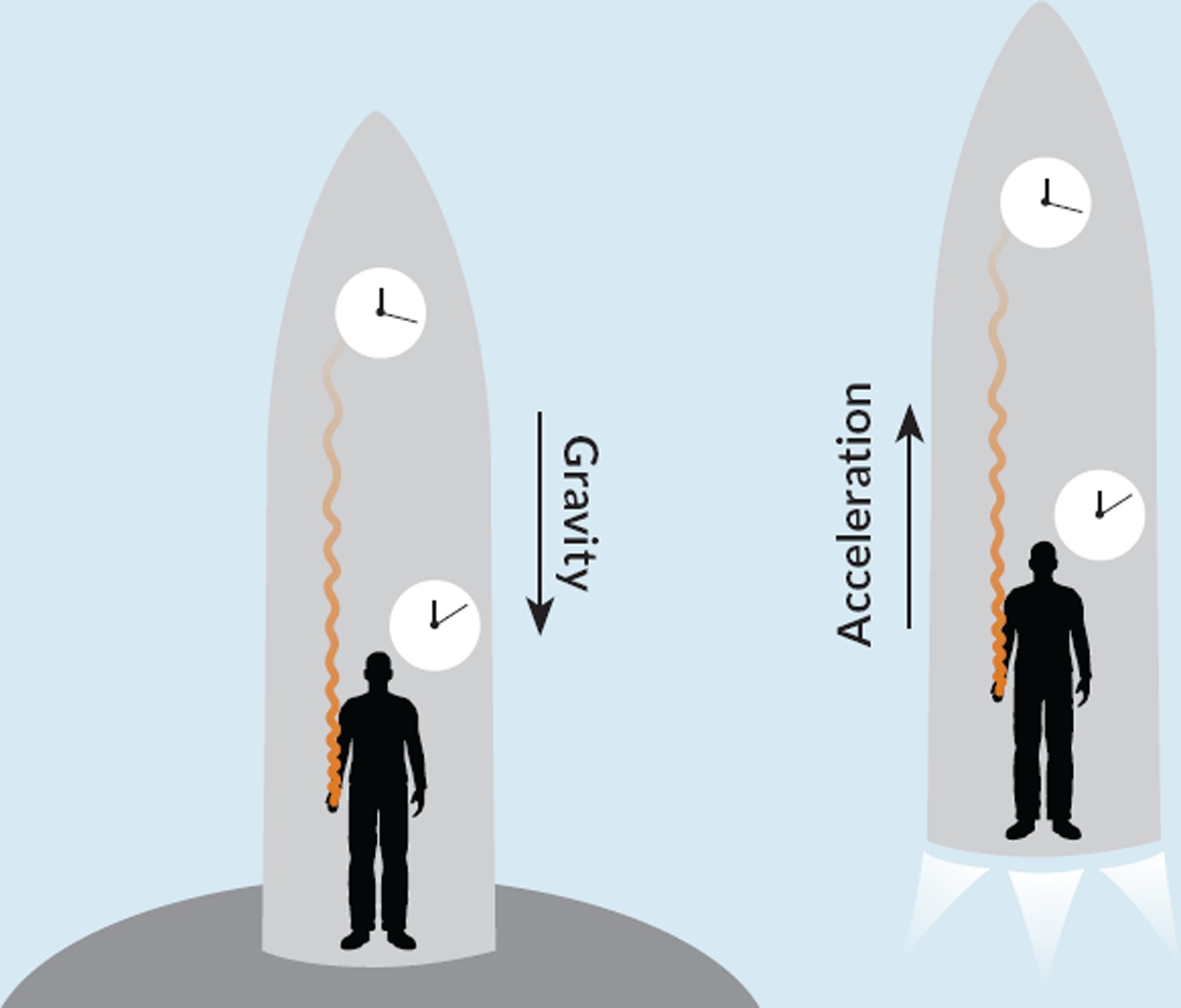
This same reasoning helps to debunk certain conspiracy theories, such as the notion of a flat Earth continuously accelerating upwards at 9.8 m/s² to simulate gravity.

If it weren’t for Einstein’s relativity, you might think that, with each second that passes by, you’d simply increase your speed by another 9.8 m/s. So how long would it take to reach the speed of light? I created a python program to answer this very question.
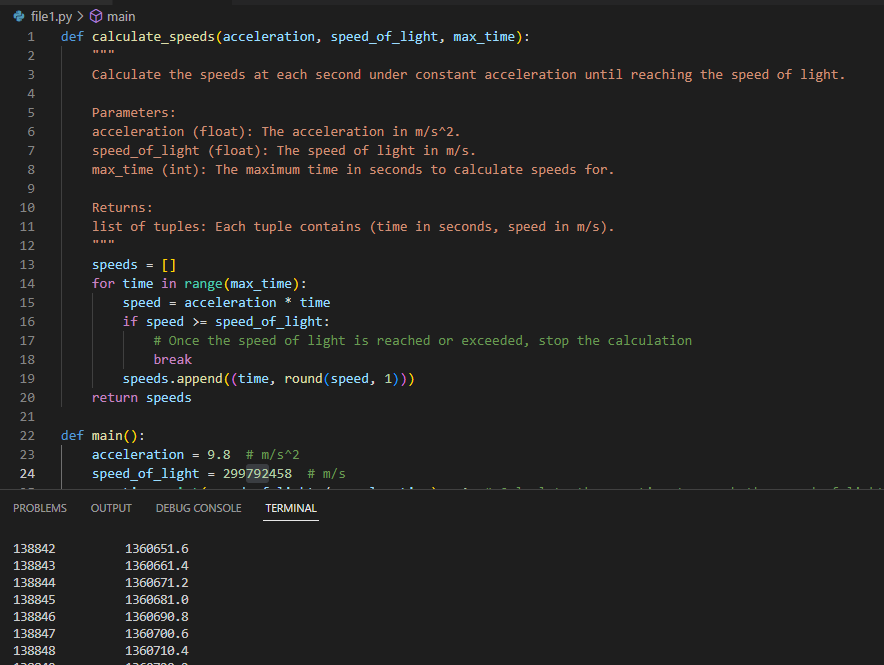
If you started off at rest, it would only take you a little less than a year — about 354 days — to reach the speed of light: 299,792,458 m/s. Even so, that this is a theoretical exercise under Newtonian physics. In reality, as an object’s speed approaches the speed of light, relativistic effects significantly alter the outcomes, preventing any object with mass from actually reaching the speed of light, so…yeah…the earth is round, and that acceleration is definitely gravity. 😊
When comparing other forces like centripetal and centrifugal forces with gravity, the common thread linking them is, again, acceleration. In a rotating space station, for example, centrifugal force provides a gravity-like sensation. As the station spins, its occupants experience an outward force – not due to any external ‘push’, but as a result of their inertia and the continuous change in direction, a kind of acceleration. This force can be calibrated to mimic Earth’s gravity by adjusting the station’s rotation rate. It’s an elegant solution to the limitations of linear acceleration in space travel.
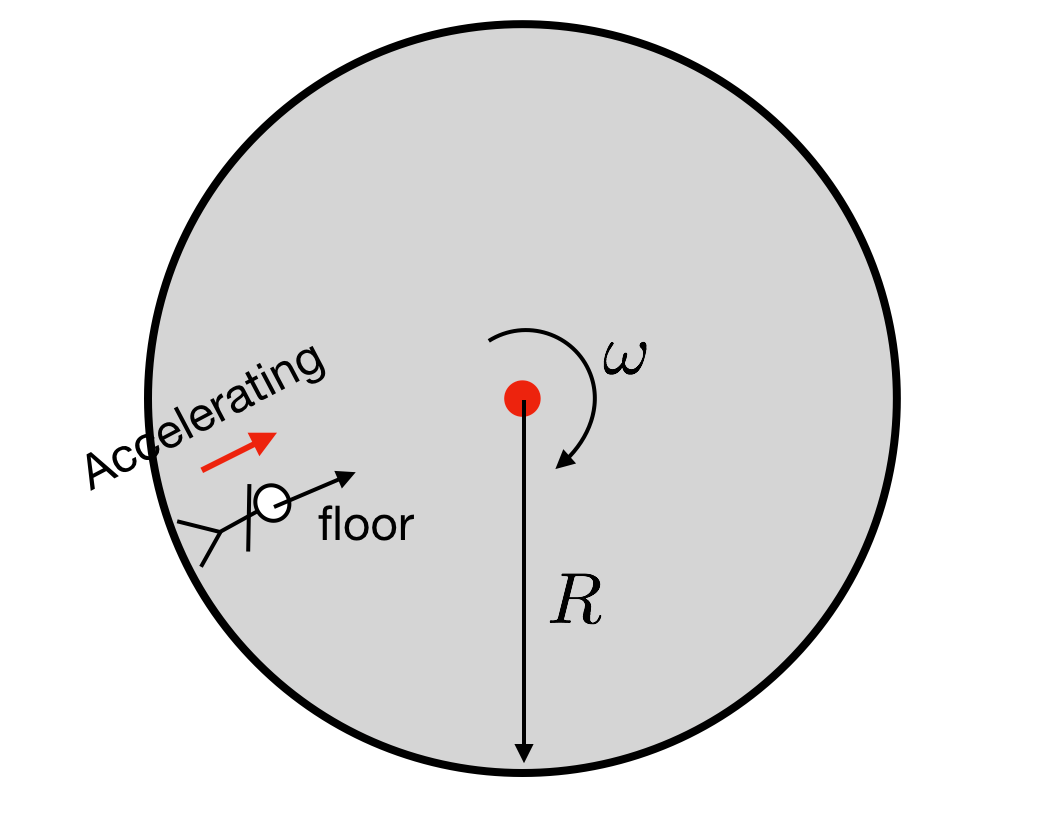
This space station, although it spins at a constant rate (it doesn’t speed up or slow down) can exert a very similar sensation to gravity as, just like with gravity, we are experiencing a constant acceleration. That is why a spinning space station (and not a constantly accelerating one) is often used in science fiction to simulate gravity. One is at least theoretically possible, whereas the other is not.
Delving deeper into the nuances of rotational dynamics, consider a ball spinning in place at a constant speed. This too experiences a constant acceleration, as remember a change in direction, just like in the example above, is acceleration. In fact, a spinning ball in place and a spinning space station are one and the same. The only difference being that you can be “inside” the ball in the space station, whereas a solid ball you cannot. The challenges of simulating gravity within a rotating object like a spinning ball are then simply because you can’t be inside the ball to be pushed towards its inner edge. Therefore, we tend to see a ball spinning in place as having acceleration being pushed away from the ball (like an “anti-gravity” of sorts), but really this is just a matter of perspective on where we want to focus on the accelerating forces. The space station, the spinning ball, and gravity all have the same force: acceleration.

This exploration of simulated gravity in various contexts not only deepens our understanding of acceleration but also illuminates the subtleties of how we experience forces. Whether it’s the constant acceleration of a spacecraft, the outward push in a spinning space station, or the outward-directed forces in a rotating ball, these forces are all about acceleration changing the velocity of objects and people. Yet, how we perceive and harness these forces can vary dramatically. These insights challenge us to think beyond traditional notions of forces and motion, recognizing acceleration as a versatile and fundamental component in the tapestry of physics. In the end, understanding and applying these concepts pushes the boundaries of technology and exploration, allowing us to adapt and thrive in environments far different from the familiar pull of Earth’s gravity.
Section 5: Relativistic and Quantum Perspectives
Delving into Einstein’s theory of relativity again, we encounter a profound shift in how we understand acceleration, especially in the context of gravity. Einstein’s General Relativity posits that what we perceive as gravitational force is actually the result of spacetime curvature. Massive objects like planets and stars warp the fabric of spacetime, and this curvature dictates the motion of objects, leading to what we interpret as acceleration due to gravity. In this framework, an object in freefall doesn’t experience force in the traditional sense; it’s merely following the natural curvature of spacetime. This interpretation aligns with our earlier discussions about acceleration being the central theme of gravitational effects. Einstein’s perspective doesn’t just enrich our understanding of gravity; it provides a broader context to view all motion and forces as interactions within spacetime, offering a more unified picture of physical laws.
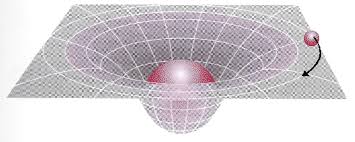
Quantum Field Theory and the Nuances of Acceleration
Quantum Field Theory (QFT) offers a profoundly different lens through which to view acceleration, particularly when juxtaposed with the more intuitive descriptions offered by classical mechanics. Quantum field theory (QFT) treats particles as excited states of their underlying quantum fields. These fields are more fundamental than the particles and can sometimes act like particles and sometimes like waves.
In the quantum realm, acceleration is less about objects speeding up or changing direction and more about the fundamental interactions at the subatomic level. QFT posits that particles are manifestations of underlying fields, and forces, including those causing acceleration, arise from the exchange of force-carrier particles, like photons in electromagnetic interactions or gluons in the strong nuclear force. This perspective radically departs from the classical notion of acceleration as a change in velocity over time, instead framing it as a consequence of quantum interactions.
Oddly, and of trouble to any physicist trying to get to the bottom of acceleration as a force, QFT can’t handle gravity, and gravity is mathematically equivalent to acceleration. If you want to go down that rabbit-hole, you will enter the attempts to unify general relativity with quantum field theory in what is known as finding a unifying or grand theory of everything.
Yet, despite its fundamental nature in QFT and Relativity, acceleration in many practical scenarios is often more conveniently and effectively understood through the lens of classical mechanics (as discussed earlier with Newtonian laws). This is because, in everyday experiences and macroscopic scales, the effects predicted by classical physics are remarkably accurate and easier to comprehend. For instance, when launching a spacecraft or constructing a building, the classical equations of motion provide sufficiently precise and practical solutions. In these cases, the fine details of quantum or relativistic interactions are not necessary to effectively describe or predict the behavior of objects under acceleration.
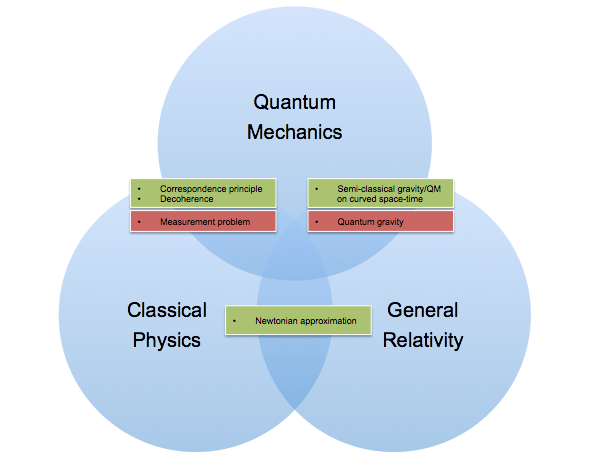
This dichotomy between QFT, relativity, and classical mechanics highlights a broader theme in physics: the need for different models to describe different scales and scenarios. While QFT offers the most fundamental understanding of forces and acceleration, its complexity and the minuscule scales at which it operates often render it less practical for everyday applications. Conversely, classical mechanics, with its more intuitive and manageable approach, provides ‘good enough’ approximations for most engineering and technological purposes. This pragmatic approach in physics underlines the importance of context and scale in choosing the right model or theory to apply, balancing the pursuit of fundamental understanding with the need for practical applicability.
Section 6: Real-World Applications and Implications
The principles of acceleration, both linear and angular, have profound applications in technology, engineering, and astronomy, shaping our world and beyond in remarkable ways. In engineering, understanding acceleration is crucial for designing vehicles, from cars that navigate city streets to spacecraft that venture off to Mars with Elon Musk inside with all of his stock in X. The ability of structures to withstand various acceleration forces determines their safety and efficiency. In the realm of technology, these principles are harnessed in devices like accelerometers, integral to smartphones and gaming controllers for motion sensing. In the expanses of astronomy, these concepts enable us to understand celestial phenomena: from the orbital mechanics of planets and moons, governed by gravitational acceleration, to the dizzying spins of neutron stars, where extreme angular acceleration plays out on a cosmic scale. Each of these applications not only leverages our understanding of acceleration but also continually refines it, as real-world scenarios provide feedback to theoretical models.
Reflecting on the philosophical and practical implications of acceleration in our understanding of the universe reveals a fascinating tapestry of interconnected concepts. Philosophically, the study of acceleration touches on the fundamental nature of reality, challenging our perceptions of motion and forces. It bridges the gap between the tangible experiences of everyday life and the abstract realms of advanced physics. Practically, these principles are a testament to the power of human inquiry and ingenuity. The ability to understand, predict, and utilize acceleration in various forms underpins much of modern technology and scientific exploration. It demonstrates our evolving mastery over the physical world, highlighting both the capabilities and limitations of our current scientific knowledge. As we continue to explore and understand these forces, we not only expand our technological horizons but also deepen our connection to the universe, appreciating the intricate laws that govern it.
Conclusion
As we conclude our exploration of acceleration and its role in simulating gravity and shaping our understanding of forces, we’re reminded of the elegance and complexity of the physical world. From the fundamental principles laid down by Newton to the revolutionary perspectives offered by Einstein, and the intricate quantum realm, each step in our journey has revealed acceleration as a central, unifying theme. It is a concept that transcends the boundaries of classical and modern physics, offering insights into everything from the engineering challenges of our daily lives to the grand scale of celestial mechanics. This journey through various perspectives of physics not only enhances our comprehension of motion and forces but also deepens our appreciation for the intricate and interconnected nature of the universe. As we continue to probe the mysteries of the cosmos and refine our technologies, the principles of acceleration will undoubtedly remain at the forefront, guiding our understanding and innovations.
Further Reading
- “Classical Mechanics” by John R. Taylor: A comprehensive textbook that provides an in-depth look at the principles of classical mechanics, including Newton’s laws and their applications.
- “Gravitation” by Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler: This seminal book offers a thorough introduction to Einstein’s general relativity, a theory that redefined our understanding of gravity and acceleration.
- “Quantum Field Theory for the Gifted Amateur” by Tom Lancaster and Stephen J. Blundell: An accessible introduction to Quantum Field Theory, explaining its fundamental concepts and implications for understanding forces and acceleration.
- NASA’s Educational Resources: NASA offers a wealth of materials on space technology, astronomy, and the physics of space travel, including the principles of acceleration in various contexts.
- The Physics Hypertextbook – Acceleration: An online resource providing a clear and concise overview of the concept of acceleration in physics.
- “Exploring Black Holes: Introduction to General Relativity” by Edwin F. Taylor and John Archibald Wheeler: This book offers an engaging exploration of black holes and the role of acceleration and gravity in their formation and behavior.
These resources provide further insights into the fascinating world of physics, delving deeper into the concepts discussed in our exploration and offering a more comprehensive understanding of acceleration and its pivotal role in the universe.





 >
> >
> >
> >
> >
> >
>