Deciphering the Intricacies of Bayesian Probability in Artificial Intelligence

In the realm of Artificial Intelligence (AI) and Machine Learning (ML), understanding the nuances of mathematical concepts is paramount for driving innovation and solving complex problems. One such concept, grounded in the discipline of probability theory, is Bayesian Probability. This mathematical framework not only offers a robust approach for making predictions but also enhances the decision-making capabilities of AI systems.

The Mathematical Framework of Bayesian Probability

Bayesian probability is a subfield of probability theory which interprets probability as a measure of belief or certainty rather than a fixed frequency. This perspective allows for updating beliefs in light of new evidence, making it an immensely powerful tool for prediction and inference in AI. The mathematical backbone of the Bayesian approach is encapsulated in Bayes’ Theorem:

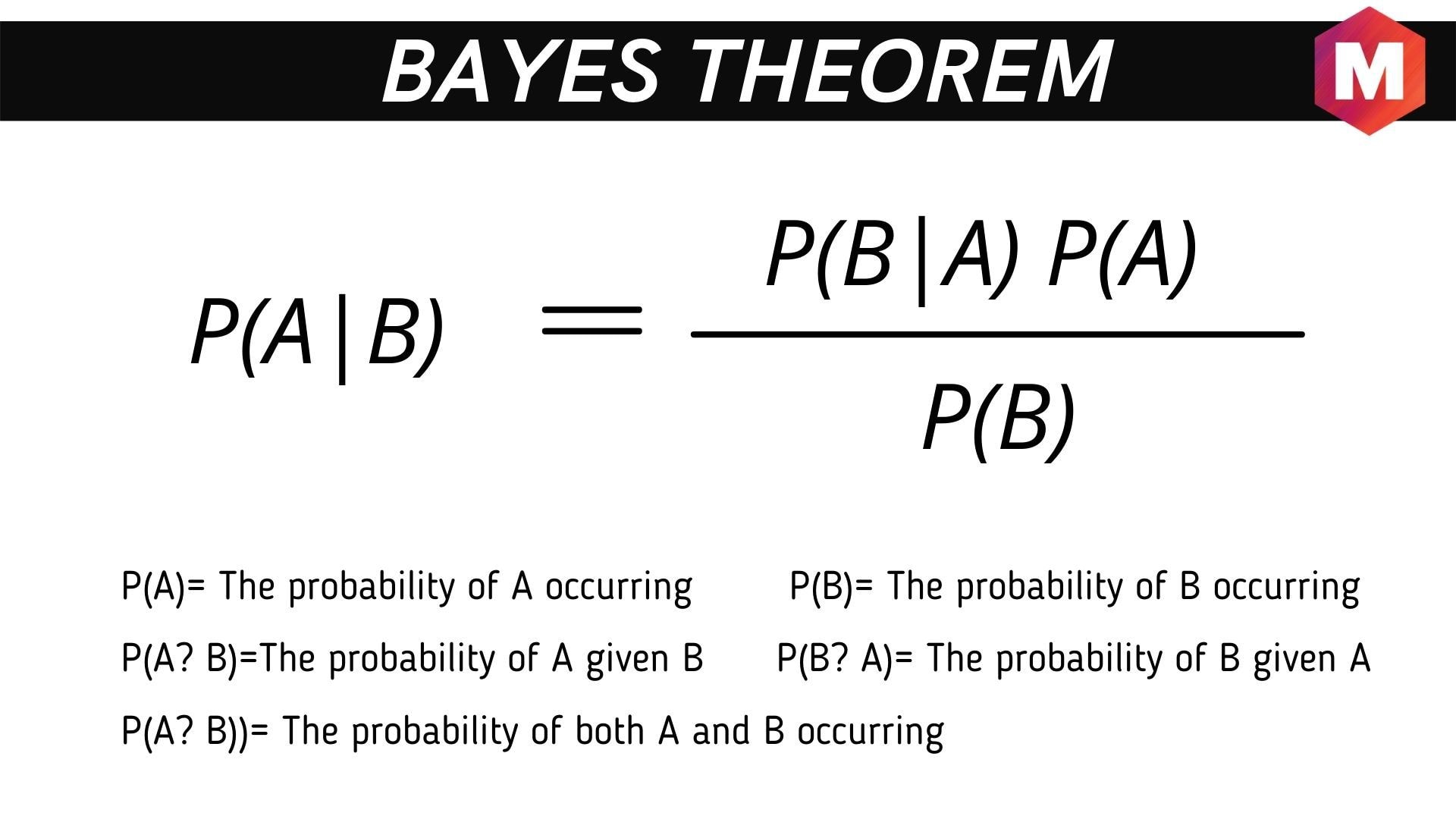
In mathematical terms, Bayes’ theorem can be expressed as:

P(A|B) = (P(B|A) * P(A)) / P(B)

Where:

• P(A|B) is the posterior probability: the probability of hypothesis A being true given that B is true.
• P(B|A) is the likelihood: the probability of observing B given hypothesis A is true.
• P(A) is the prior probability: the initial probability of hypothesis A being true.
• P(B) is the marginal probability: the total probability of observing B.

Application in Artificial Intelligence

My work at DBGM Consulting, Inc., particularly in AI workshops and the development of machine learning models, heavily relies on the principles of Bayesian probability. A hallmark example is its application in predictive machines, such as chatbots and self-driving robots, which my team and I have developed using Bayesian frameworks for enhanced decision-making capabilities.

Consider a chatbot designed to provide customer support. Utilizing Bayesian probability, it can update its responses based on the interaction history with the customer, thereby personalizing the conversation and increasing the accuracy of its support.

Furthermore, Bayesian probability plays a crucial role in the development of self-driving robots. By continuously updating the robot’s knowledge base with incoming sensor data, we can predict potential hazards and navigate effectively—an application witnessed in my AI-focused projects at Harvard University.

Probability Theory in the Context of Previous Articles

Relating the principles of Bayesian Probability to my earlier discussions on the mathematical foundations of large language models, it’s evident that probability theory is paramount across the spectrum of AI research and development. Similar to how prime factorization in number theory secures cloud technologies, Bayesian inference ensures the AI’s decisions are both rational and data-driven.

Conclusion

Beyond its application in AI, Bayesian probability reminds us of the power of adaptability and learning from new experiences—a principle I embody in both my professional and personal pursuits. Whether it’s in crafting AI solutions at DBGM Consulting or delving into the mysteries of the cosmos with my amateur astronomer friends, the Bayesian approach provides a mathematical foundation for evolving our understanding with every new piece of evidence.

As we continue to explore the intricate dance between AI and mathematics, it becomes increasingly clear that the future of technological innovation lies in our ability to intertwine complex mathematical theories with practical AI applications. Bayesian probability is but a single thread in this vast tapestry, yet it’s one that weaves through many of the advances we see today in AI and beyond.

Focus Keyphrase: Bayesian Probability in AI