Understanding the Monty Hall Problem: Insights for AI and ML
Demystifying the Monty Hall Problem: A Probability Theory Perspective
As someone deeply entrenched in the realms of Artificial Intelligence (AI) and Machine Learning (ML), I often revisit foundational mathematical concepts that underpin these technologies. Today, I’d like to take you through an intriguing puzzle from probability theory known as the Monty Hall problem. This seemingly simple problem offers profound insights not only into the world of mathematics but also into decision-making processes in AI.
Understanding the Monty Hall Problem
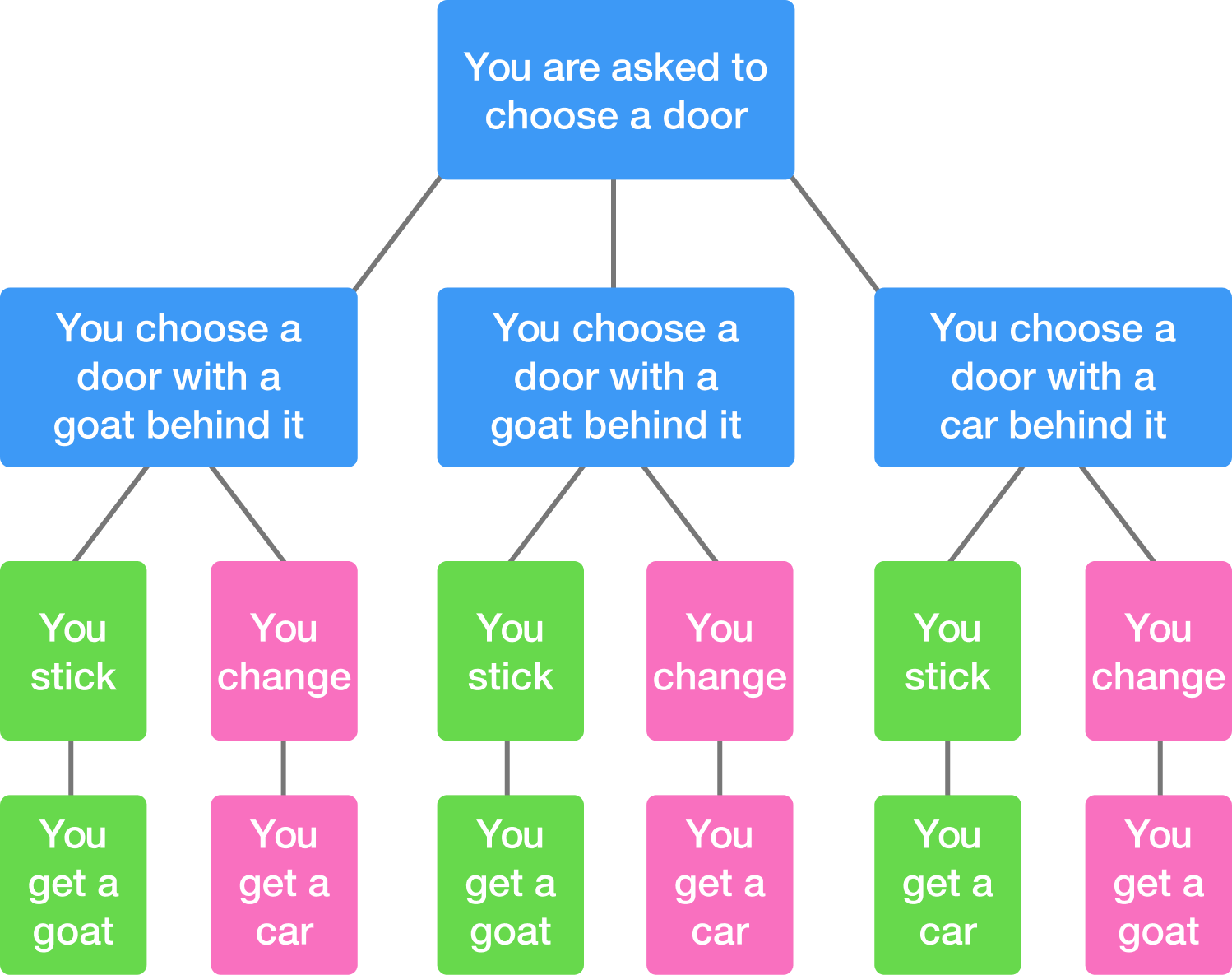
The Monty Hall problem is based on a game show scenario where a contestant is presented with three doors. Behind one door is a coveted prize, while the other two conceal goats. The contestant selects a door, and then the host, who knows what’s behind each door, opens one of the remaining doors to reveal a goat. The contestant is then offered a chance to switch their choice to the other unopened door. Should they switch?
Intuitively, one might argue that it doesn’t matter; the odds should be 50/50. However, probability theory tells us otherwise. The probability of winning by switching is actually 2/3, while staying with the original choice gives a probability of 1/3 of finding the car.
The Math Behind It
The initial choice of the door has a 1/3 chance of being the prize door and a 2/3 chance of being a goat door. When the host opens another door to reveal a goat, the 2/3 probability of the initial choice being incorrect doesn’t just vanish; instead, it transfers to the remaining unopened door. Thus, switching doors leverages the initial probability to the contestant’s advantage.
Formally, this can be represented as:
- P(Win | Switch) = P(Goat initially chosen) × P(Host reveals goat | Goat initially chosen) × P(Switch to Car)
- Which simplifies to: 2/3
- P(Win | Stay) = P(Car initially chosen) × P(Host reveals goat | Car initially chosen) × P(Stay)
- Which simplifies to: 1/3
These probabilities provide a stark illustration of how our intuitions about chance and strategy can sometimes mislead us, a lesson that’s crucial in the development and tuning of AI algorithms.
Application in AI and Machine Learning
In AI, decision-making often involves evaluating probabilities and making predictions based on incomplete information. The Monty Hall problem serves as a metaphor for the importance of revising probabilities when new information is available. In Bayesian updating, a concept closely related to structured prediction in machine learning, prior probabilities are updated in the light of new, relevant data – akin to the contestant recalculating their odds after the host reveals a goat.
This principle is pivotal in scenarios such as sensor fusion in robotics, where multiple data sources provide overlapping information about the environment, and decisions must be continuously updated as new data comes in.
Revisiting Previous Discussions
In my exploration of topics like Structured Prediction in Machine Learning and Bayesian Networks in AI, the underlying theme of leveraging probability to improve decision-making and predictions has been recurrent. The Monty Hall problem is a testament to the counterintuitive nature of probability theory, which continually underscores the development of predictive models and analytical tools in AI.
Conclusion
As we delve into AI and ML’s mathematical foundations, revisiting problems like Monty Hall reinvigorates our appreciation for probability theory’s elegance and its practical implications. By challenging our intuitions and encouraging us to look beyond the surface, probability theory not only shapes the algorithms of tomorrow but also refines our decision-making strategies in the complex, uncertain world of AI.
For AI professionals and enthusiasts, the Monty Hall problem is a reminder of the critical role that mathematical reasoning plays in driving innovations and navigating the challenges of machine learning and artificial intelligence.
Reflection
Tackling such problems enhances not only our technical expertise but also our philosophical understanding of uncertainty and decision-making – a duality that permeates my work in AI, photography, and beyond.
As we move forward, let’s continue to find inspiration in the intersection of mathematics, technology, and the broader questions of life’s uncertain choices.









Although I’m somewhat skeptical about where AI is going, this piece on the Monty Hall problem was enlightening. It’s a good reminder of how foundational mathematical concepts are crucial to AI’s development. As a network engineer, I appreciate the thorough breakdown and its application in AI decision-making processes.
Hi everyone, David here. I wanted to share this exploration of the Monty Hall problem because it beautifully illustrates the critical role of probability theory in AI and ML. It’s a fascinating subject that challenges our intuitions and has profound implications for decision-making in technology. Hope you find it as intriguing as I do!