Unlocking the Power of Dimensionality Reduction in Machine Learning

In recent discussions, we’ve delved deep into the transformative world of Artificial Intelligence (AI) and Machine Learning (ML), exploring large language models, their applications, and the promise they hold for the future. Continuing on this path, today’s focus shifts towards an equally critical yet often less illuminated aspect of machine learning: Dimensionality Reduction. This technique plays a vital role in preprocessing high-dimensional data to enhance model performance, reduce computational costs, and provide deeper insights into data analysis.

Understanding Dimensionality Reduction

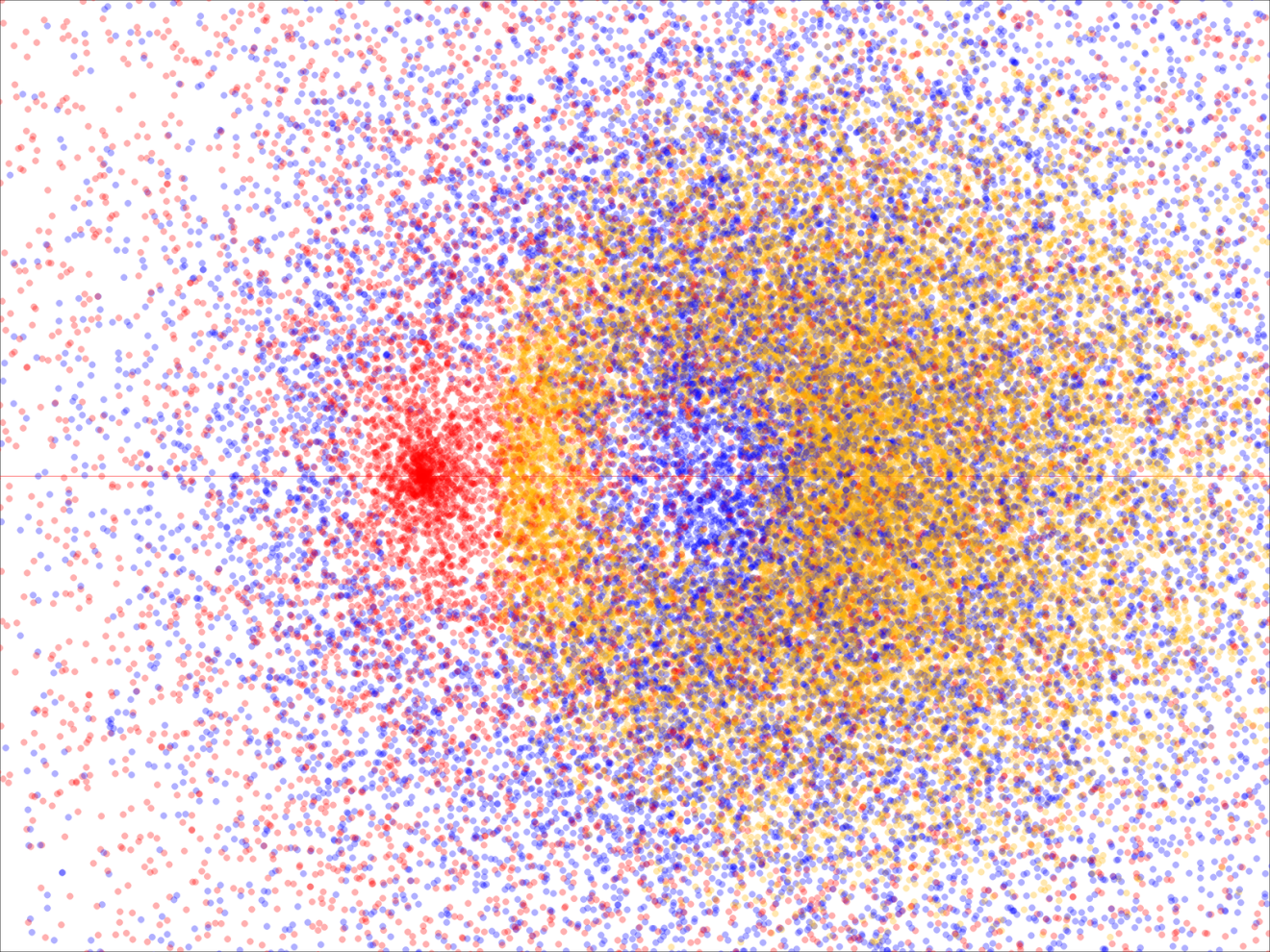
Dimensionality reduction is a technique used to reduce the number of input variables in your dataset. In essence, it simplifies the complexity without losing the essence of the information. The process involves transforming data from a high-dimensional space to a lower-dimensional space so that the reduced representation retains some meaningful properties of the original data, ideally close to its intrinsic dimensionality.

<>

High-dimensional data, often referred to as “the curse of dimensionality,” can significantly hamper the performance of ML algorithms. Not only does it increase the computational burden, but it can also lead to overfitting, where the model learns the noise in the training data instead of the actual signal. By employing dimensionality reduction, we can mitigate these issues, leading to more accurate and efficient models.

Techniques of Dimensionality Reduction

Several techniques exist for dimensionality reduction, each with its approach and application domain.

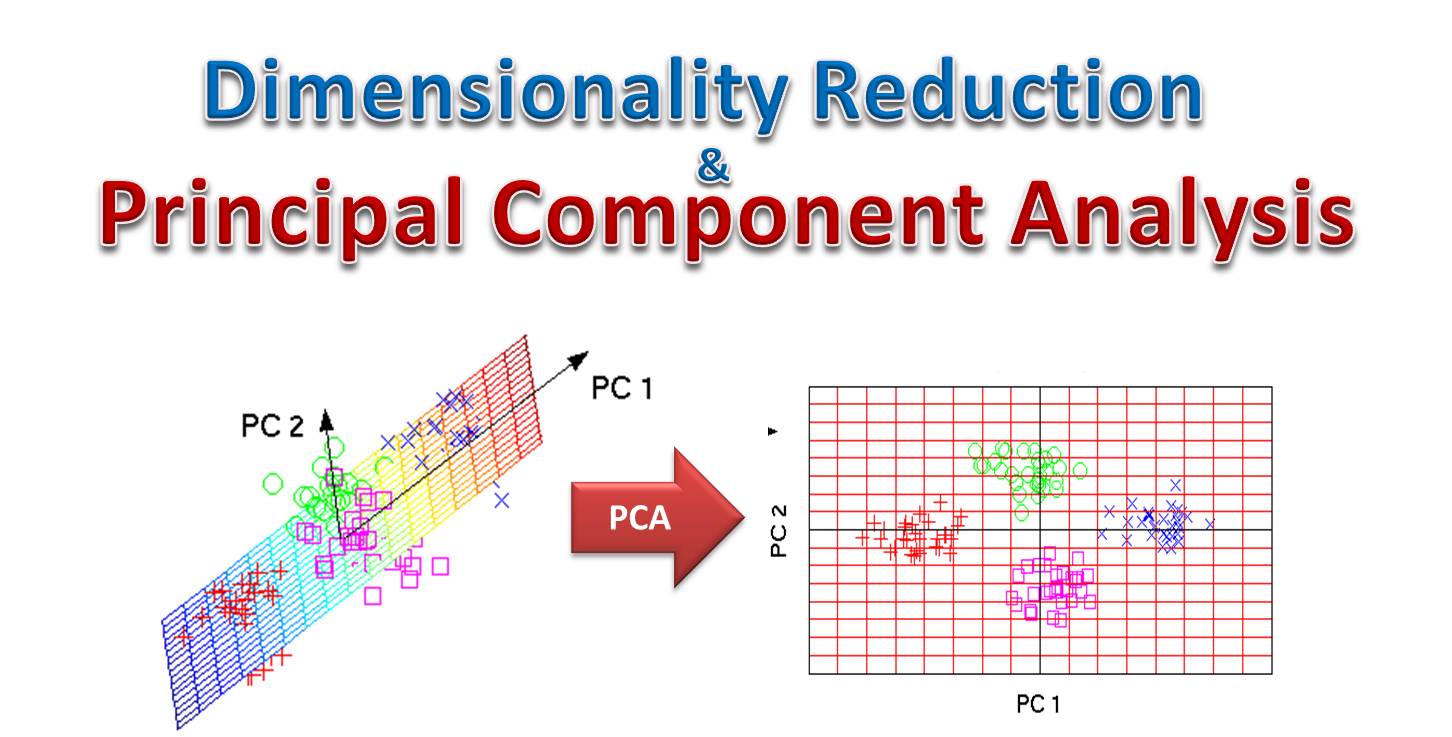
• Principal Component Analysis (PCA): PCA is one of the most widely used techniques. It works by identifying the directions (or principal components) that maximize the variance in the data.
• t-Distributed Stochastic Neighbor Embedding (t-SNE): t-SNE is a technique particularly well-suited for the visualization of high-dimensional datasets. It works by converting the data into two or three dimensions while preserving the small pairwise distances or local similarities between points.
• Linear Discriminant Analysis (LDA): LDA is used as a dimensionality reduction technique in the pre-processing step for pattern-classification and machine learning applications. It aims to find a linear combination of features that characterizes or separates two or more classes.

Each of these techniques offers a unique approach to tackling the challenges posed by high-dimensional data, and the choice of method depends largely on the specific requirements of the task at hand.

Applications and Importance

The benefits of dimensionality reduction are vast and varied, impacting numerous domains within the field of machine learning and beyond.

• Data Visualization: Reducing dimensionality to two or three dimensions makes it possible to plot and visually explore complex datasets.
• Speeding up Algorithms: Lower-dimensional data means faster training times for machine learning models without significant loss of information, leading to more efficient algorithm performance.
• Improved Model Performance: By eliminating irrelevant features or noise, dimensionality reduction can lead to models that generalize better to new data.

<>

In my own journey, especially during my time at Harvard focusing on AI and Machine Learning, I worked intensively with high-dimensional data, employing techniques like PCA and t-SNE to extract meaningful insights from complex datasets. This experience, coupled with my involvement in AI through DBGM Consulting, Inc., has reinforced my belief in the transformative power of dimensionality reduction in unlocking the potential of machine learning models.

Looking Ahead

As we continue to push the boundaries of what’s possible in AI and ML, the role of dimensionality reduction will only grow in importance. The challenge of managing high-dimensional data isn’t going away, but through techniques like PCA, t-SNE, and LDA, we have powerful tools at our disposal to tackle this issue head-on.

Moreover, the ongoing development of new and improved dimensionality reduction techniques promises to further enhance our ability to process, analyze, and draw insights from complex datasets. As these methods become more sophisticated, we can expect to see even greater advancements in machine learning applications, from natural language processing to computer vision and beyond.

<>

In conclusion, dimensionality reduction is a cornerstone technique in the field of machine learning, essential for handling the vast and complex datasets that define our digital age. By simplifying data without sacrificing its integrity, we can build more accurate, efficient, and insightful models—clearing the path for the next wave of innovations in AI.

I encourage fellow enthusiasts and professionals in the field to explore the potential of dimensionality reduction in their work. As evidenced by our past explorations into AI and ML, including the intricate workings of artificial neural networks, the journey of unraveling the mysteries of machine learning continues to be a rewarding endeavor that drives us closer to the future we envision.